Loading... <div class="tip inlineBlock warning"> 吴恩达 · 机器学习课程 地址:[有监督的机器学习:回归与分类](https://www.coursera.org/learn/machine-learning) </div> # 1、机器学习绪论 ## 1.1 机器学习导言 本课程将讲授最先进的机器学习技术,包括最重要的算法和实用技巧,以及机器学习在今天的广泛应用和在人工智能领域的重要性。除此之外,课程还会探讨人工通用智能的相关内容,以及机器学习在未来的潜力和价值。 机器学习在许多领域都有广泛的应用。例如,搜索引擎可以通过机器学习技术来提高搜索结果的准确性和相关性。在社交媒体方面,机器学习可以帮助提高用户体验和个性化推荐。医疗保健领域也可以使用机器学习来帮助诊断和治疗疾病。此外,机器学习在工业应用中也有广泛应用,例如优化生产过程和预测设备故障。 ## 1.2 机器学习定义 机器学习可以分为两类:监督学习和无监督学习。监督学习是指使用有标记的数据来训练模型,以便能够对新数据进行预测。无监督学习则是在没有标记的数据中学习模型。 阿瑟 · 塞缪尔(Arthur Samuel 1959年)\~ Machine Learning: Field ofstudy that gives computers the ability to learnwithout being explicitly programmed. 汤姆 · 米切尔(Tom Mitchell 1998年)\~ Well-posed Learning: A computer program is said to learnfrom experience E with respect to some task Tand some performance measure P, if its performance on T, as measured by'P, improveswith experience E. * **T:任务**,机器帮助人们解决的问题 * **P:性能**,机器所能做到的程度 * **E:经验**,人们输入的实践经验 ## 1.3 监督学习(Supervised Learning) 监督学习是机器学习中的一种方法,可用于预测未知数据的输出,通过给计算机提供一组输入和输出对,让计算机从中学习一个函数,以便能够对新的输入进行预测。监督学习可以用于分类和回归问题。 <div class="tip inlineBlock info simple"> 💡 Learns from being given "right answers”. input($x$) → output label ($y$) </div> 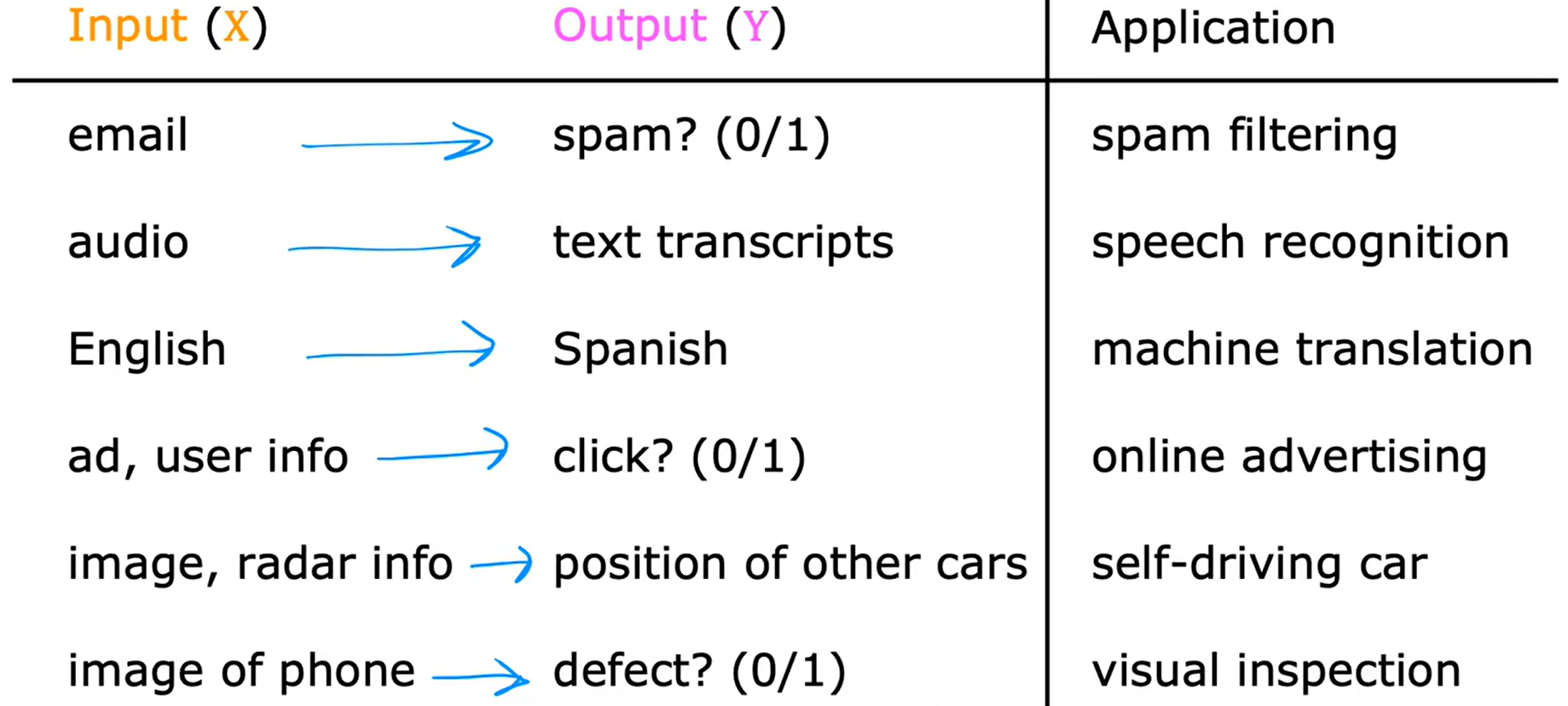 ### ① 回归问题(Regression Problem):房价预测 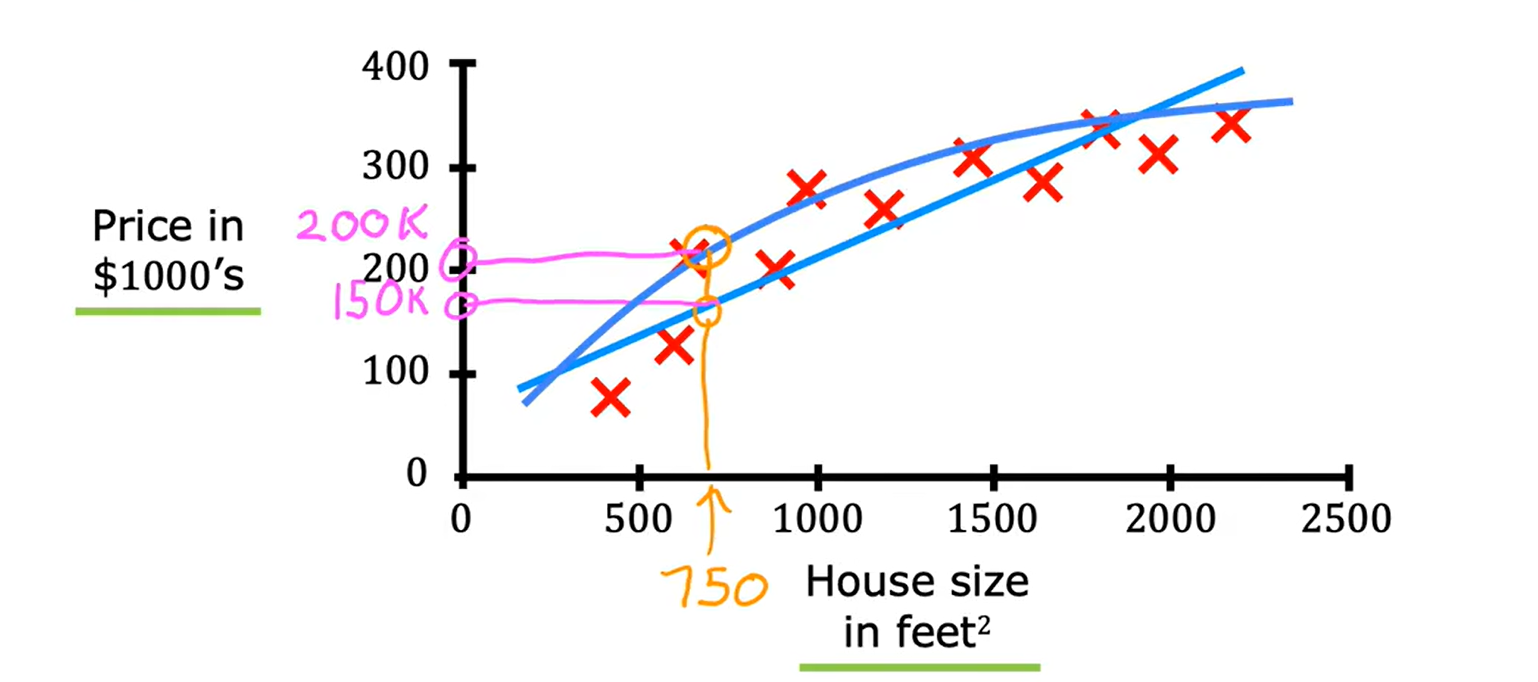 回归问题是指基于给定的数据集中包含的正确价格或标签,使用算法来预测一个连续的数值型结果。通常使用线性回归等算法来拟合数据,以便找到最适合数据的线或曲线。 ### ② 分类问题(Classification Problem):乳腺癌检查 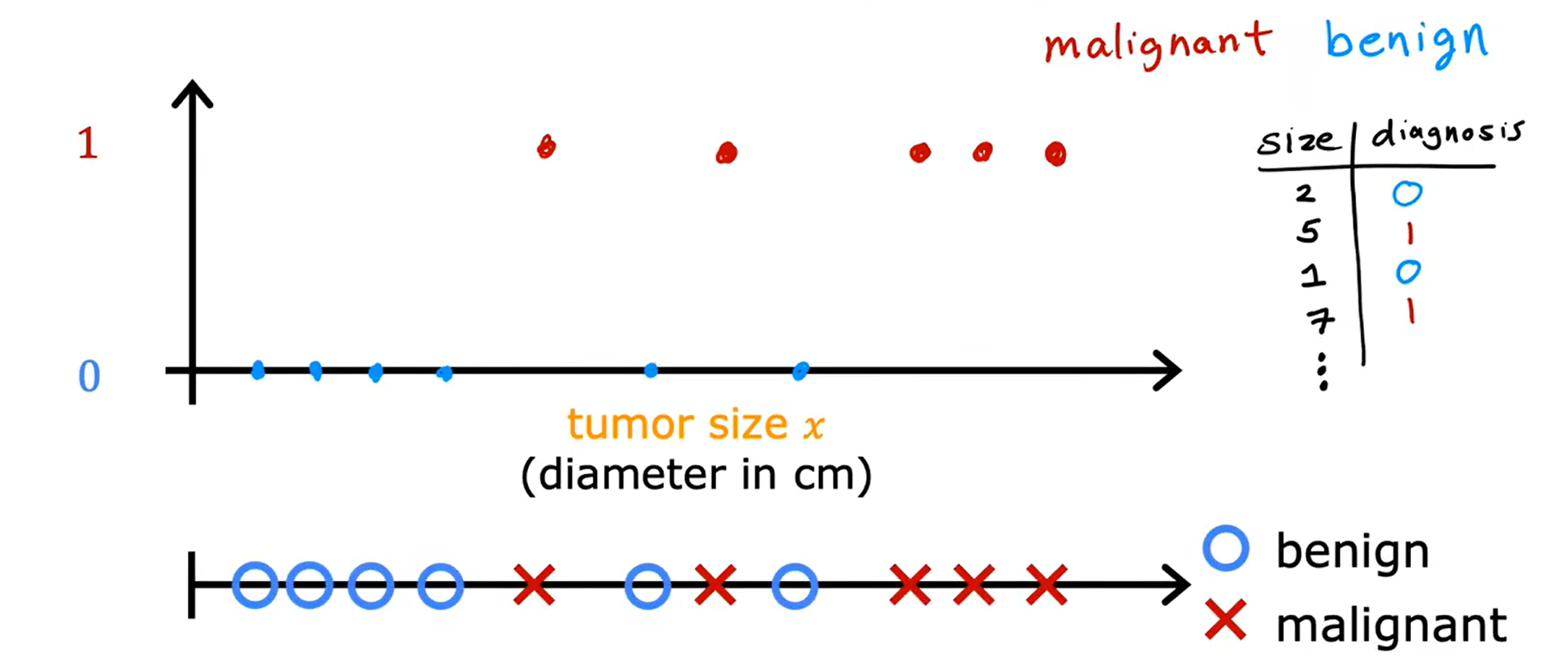 二分类是一种机器学习任务,旨在将给定的输入数据分成两个不同的类别中的一个。而上图表示的仅有癌症良性和恶性两类,因此属于二分类问题。  输出的种类可能并不是只有两种,还包括其他种类,那么这就变成了一个多分类问题,多分类问题是一种机器学习任务,旨在将给定的输入数据分成三个或三个以上的不同类别中的一个。 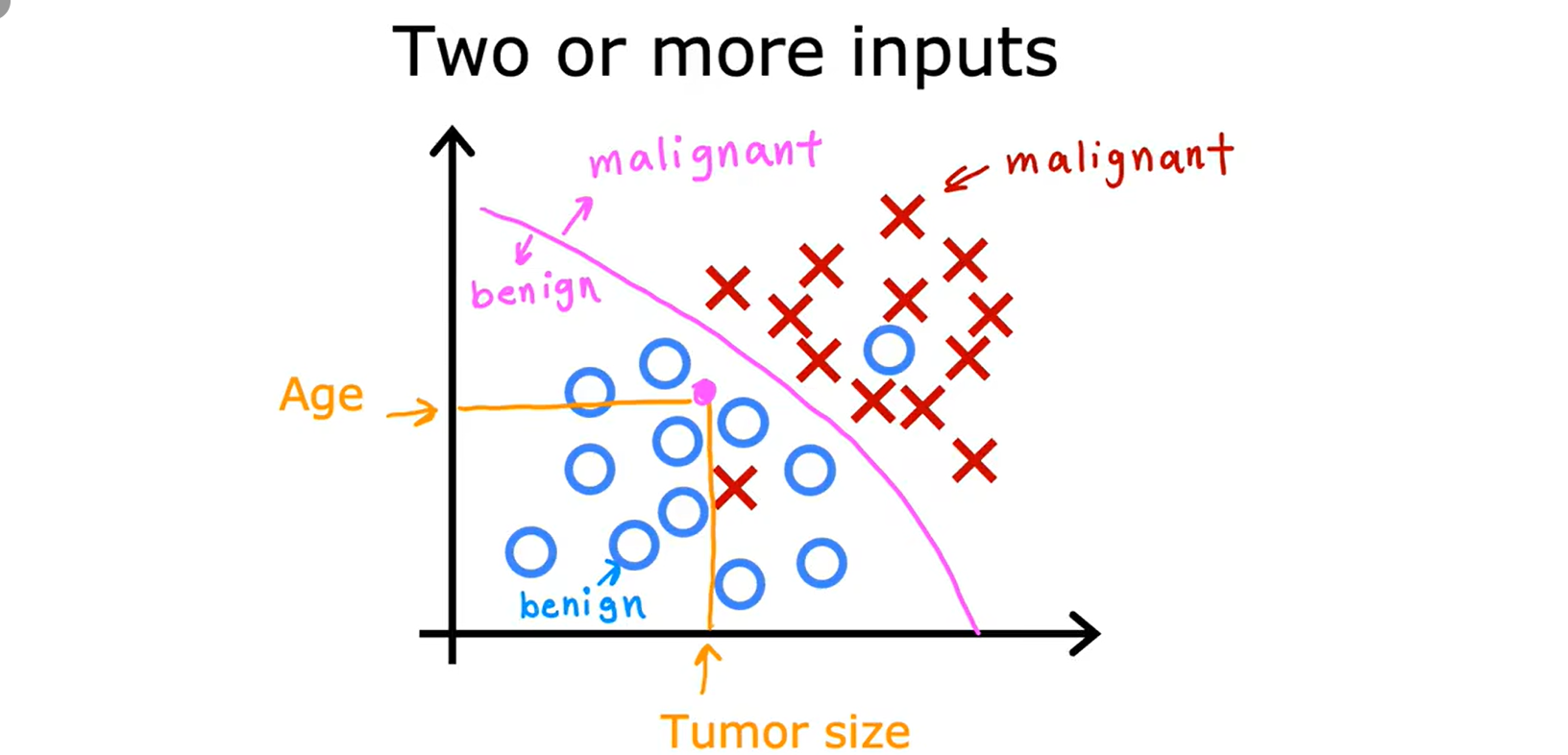 在分类问题中,我们的输入可能不止一个而是存在多个输入。例如,对于肿瘤预测问题,我们可以使用多个输入,如肿瘤大小、肿块的厚度、细胞大小的均匀性、细胞形状的均匀性等等。这些输入值可以帮助机器学习算法拟合分类的边界线,以便更准确地预测肿瘤是良性还是恶性的,因此也可以通过上图样式表示分类问题。 ### 监督学习 ~ 总结(Summery)  ## 1.4 无监督学习(Unsupervised Learning) 无监督学习是一种学习方法,它从没有标记的数据中学习模型。在无监督学习中,计算机需要自己发现数据中的模式和结构。无监督学习可以用于聚类、降维和关联规则挖掘等问题。 <div class="tip inlineBlock share simple"> 💡 Data only comes with inputs $x$, but not output labels $y$. </div>  ### ① 聚类(Custering) 聚类算法的作用是将数据集中相似的数据分组聚集在一起,聚类算法不需要事先知道数据集中的类别或标签,也不需要人工标注数据。 1. 谷歌新闻中的聚类是将包含相似关键词的文章分组聚集在一起。 2. DNA 数据聚类是将具有相似基因或DNA活动的人分组聚集在一起。 3. 客户分组则是将具有相同动机的用户分组到同一群组中,发现细分市场。 ### ② 异常检测(Anomaly Detection) 异常检测主要用于检测数据中的异常事件,如金融系统中的欺诈交易等。 ### ③ 降维(Dimensionality) 降维它可以将大规模数据集压缩成小规模数据集,同时尽可能地减少信息丢失。 ## 1.5 监督学习 VS 无监督学习 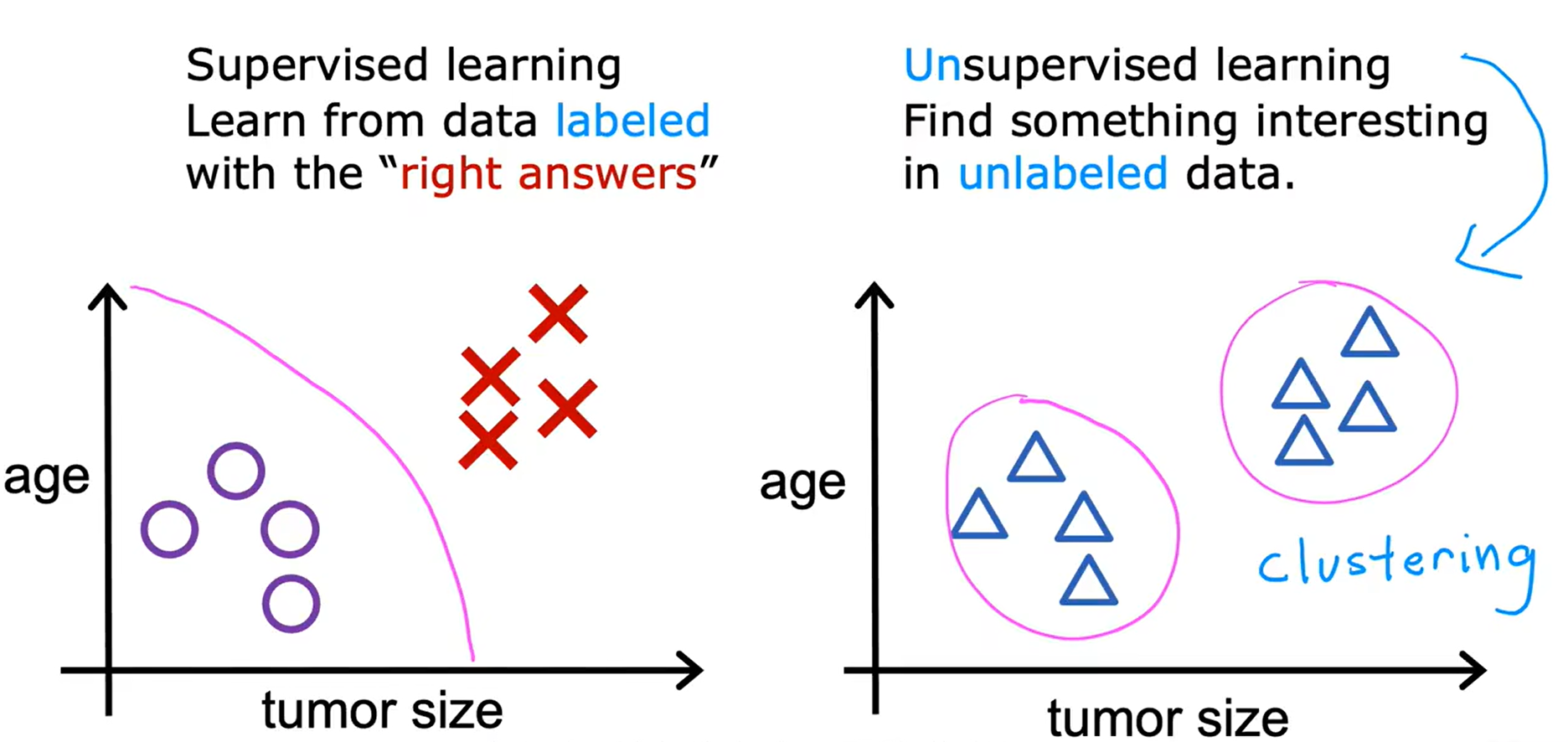 | **监督学习** | **非监督学习** | | --------------------------------- | -------------------------------- | | 每个样本都与一个输出标签 y 相关联 | 数据与任何输出标签 y 都没有关联 | | 旨在训练模型将输入映射到输出 | 旨在发现数据的模式和结构 | | 常用于分类、回归等任务 | 常用于聚类、异常检测、降维等任务 | ## 1.6 Jupyter Notebook Jupyter Notebook 是机器学习和数据科学从业者使用最广泛的工具之一,它是一个写代码、做实验的开发环境。在 Jupyter Notebook 中,用户可以使用浏览器构建一个开发环境,并测试自己的想法。这个工具并不是简化后的开发环境,用户可以使用和许多大国开发人员同款的开发环境。 > 具体内容不做讲解,自行学习相关使用方法,Colab 地址:[https://colab.research.google.com/](https://colab.research.google.com/) # 2、单变量线性回归 线性回归是一种监督学习方法,它可以用于预测连续值输出的问题。线性回归试图在输入变量和输出变量之间建立一条直线性关系。在本周的课程中,我们将学习如何使用梯度下降算法来优化线性回归模型。 ## 2.1 线性回归模型(Linear Regression Model) ### 回归模型 & 分类模型 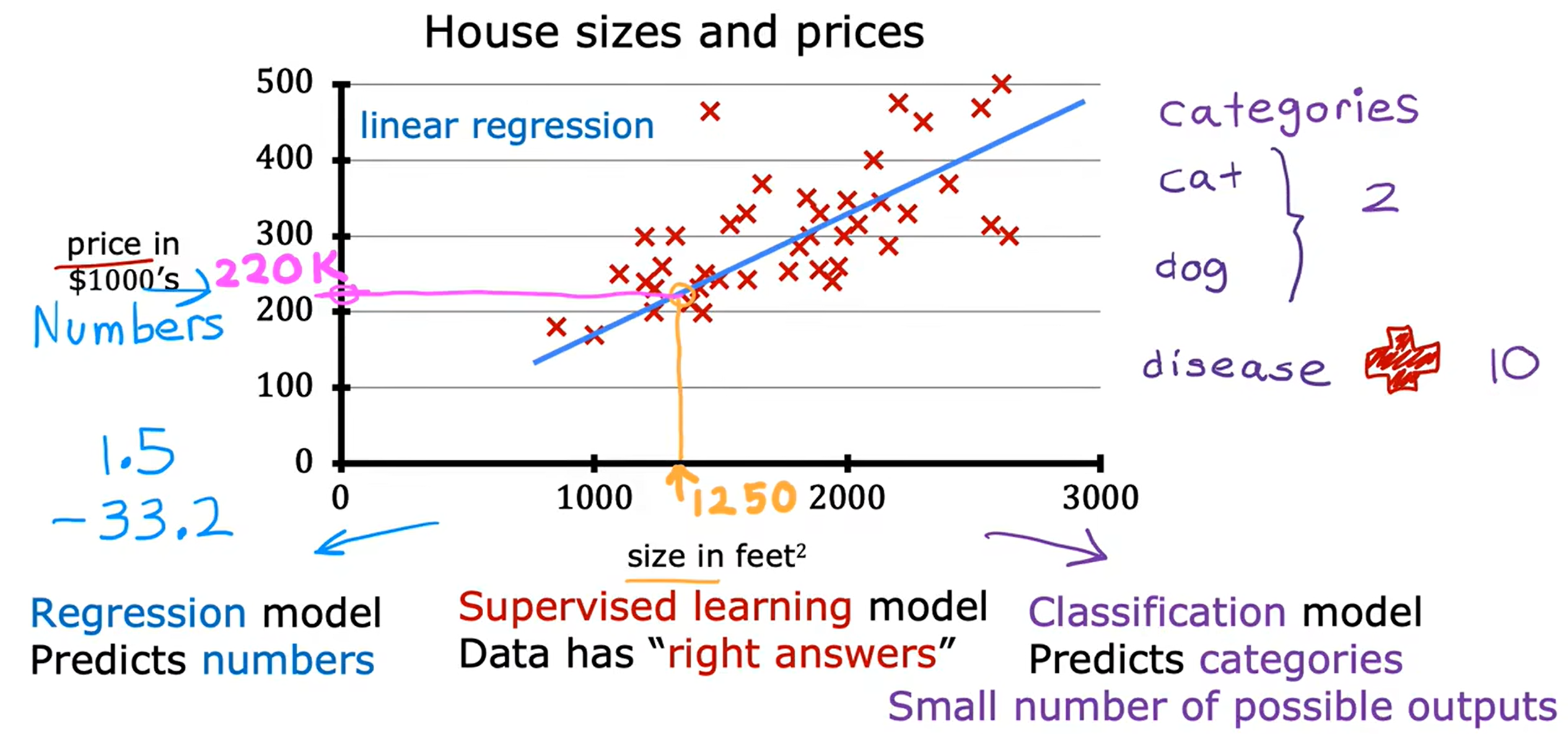 | **模型类型** | **解决问题** | **输出类型** | **示例** | | ------------ | ------------ | ------------ | ----------------------- | | 回归模型 | 回归问题 | 数字 | 价格预测 | | 分类模型 | 分类问题 | 离散类别 | 猫/狗图像分类、疾病预测 | ### 机器学习 ~ 术语(Terminology)  | **术语** | **定义** | | -------- | ------------------------------------------------------------------------- | | 训练集 | 用于训练模型的数据集 | | 验证集 | 用于评估模型的泛化能力和调整模型超参数的数据集 | | 输入特征 | 在机器学习中,表示输入的标准符号是小写$x$,也称为输入特征或特征 | | 目标变量 | 在机器学习中,表示你想要预测的输出变量的标准符号是小写$y$,也称为目标变量 | | 样本 | 数据集中的一个单独的数据项,也称为示例或数据点 | | 训练样本 | 用于训练模型的样本 | | 验证样本 | 用于评估模型的泛化能力和调整模型超参数的样本 | | 测试样本 | 用于评估模型在未见过数据上的性能的样本 | | 总样本数 | 用小写m表示,指训练集或数据集中的总样本数 | ### 线性回归模型(Linear Regression Model) 线性回归是一种经典的机器学习算法,用于建立输入特征(features)和目标变量(targets)之间的线性关系。它的目标是通过学习输入特征与目标变量之间的线性关系来预测新数据点的目标变量。 $$ f_{w,b}(x) = w * x + b $$ 线性回归模型的基本假设是输入特征与目标变量之间存在线性关系,即目标变量可以表示为输入特征的线性组合。在简单线性回归中,只有一个输入特征,可以表示上述公式,其中 $y$ 表示目标变量,$x$ 表示输入特征,$w$ 表示权重,$b$ 表示偏置。模型的目标是找到最优的权重 $w$ 和偏置 $b$,使得模型的预测值与真实值之间的误差最小化。 ## 2.2 代价函数(Cost Function) ### 线性回归模型 ~ 参数(paremeters) $$ f_{w,b}(x) = w * x + b $$ 在线性回归模型中,$w$ 和 $b$ 被称为模型的参数(paremeters),而在机器学习的训练过程中,我们可以通过调整模型的参数变量来改进模型。 而在线性回归模型的图像中,我们不难发现,$w$ 即为图像的斜率(slope),而 $b$ 即为图像的截距(intercept)。在训练模型时,我们需要选择适当的参数 $w$ 和 $b$ 的值,使得从函数 $f$ 得到的直线可以很好地拟合数据。 ### 平方误差损失函数(Squared Error Cost Function) > Cost Function:代价函数 = 损失函数 = 成本函数 为了衡量一条直线与训练数据的吻合程度,需要构造一个代价函数。而计算代价函数需要比较预测值 $\hat{y}$ 和目标值 $y$ 之间的差异,这个差异称为误差,为了衡量误差,需要计算误差的平方。 同时,为了避免训练集过大导致代价函数过大,通常使用均方误差代替总平方误差,并将其除以训练集大小 $m$。此外,根据惯例,代价函数会除以 $2m$,以便后续计算更加简便。 <div class="tip inlineBlock warning simple"> 🧐 可以在查看梯度下降部分,为什么要除 2m。 </div> 代价函数通常表示为 $J(w,b)$ 或平方误差损失函数(Squared Error Cost Function),在线性回归模型中是最常用的一个代价函数。 $$ J(w,b) = \frac{1}{2m}\sum_{i=1}^{m}(\hat{y}^{(i)} - y^{(i)})^2 $$ 其中,$m$ 是训练集中样本的数量,$y$ 表示真实目标变量的值,$\\hat{y}$ 表示模型的预测值。故可以将预测值替换为 $f_{w,b}(x)$,得到下面公式: $$ J(w,b) = \frac{1}{2m}\sum_{i=1}^{m}(f_{w,b}(x^{(i)}) - y^{(i)})^2 $$ ### 理解代价函数 关于如何更好地形象化代价函数 $J$,首先,我们使用简化的线性回归模型方程 $f_w(x)=w*x$,使其参数 $b$ 被移除或设为 0。这样,代价函数 $J$ 只有一个参数 $w$,并且它的式子和之前的类似,是对模型预测值和真实值之间的平方误差的求和。因此,我们的目标是找到使得 $J$ 最小化的 $w$ 值,而不是 $w$ 和 $b$ 的值。 通过画出代价函数 $J$ 关于 $w$ 的图像,我们可以看到,在本例子中令 $w=1$ 是一个不错的选择,因为这样能够最小化平方误差,并得到一个很好的模型,即得到了与训练数据非常吻合的直线。 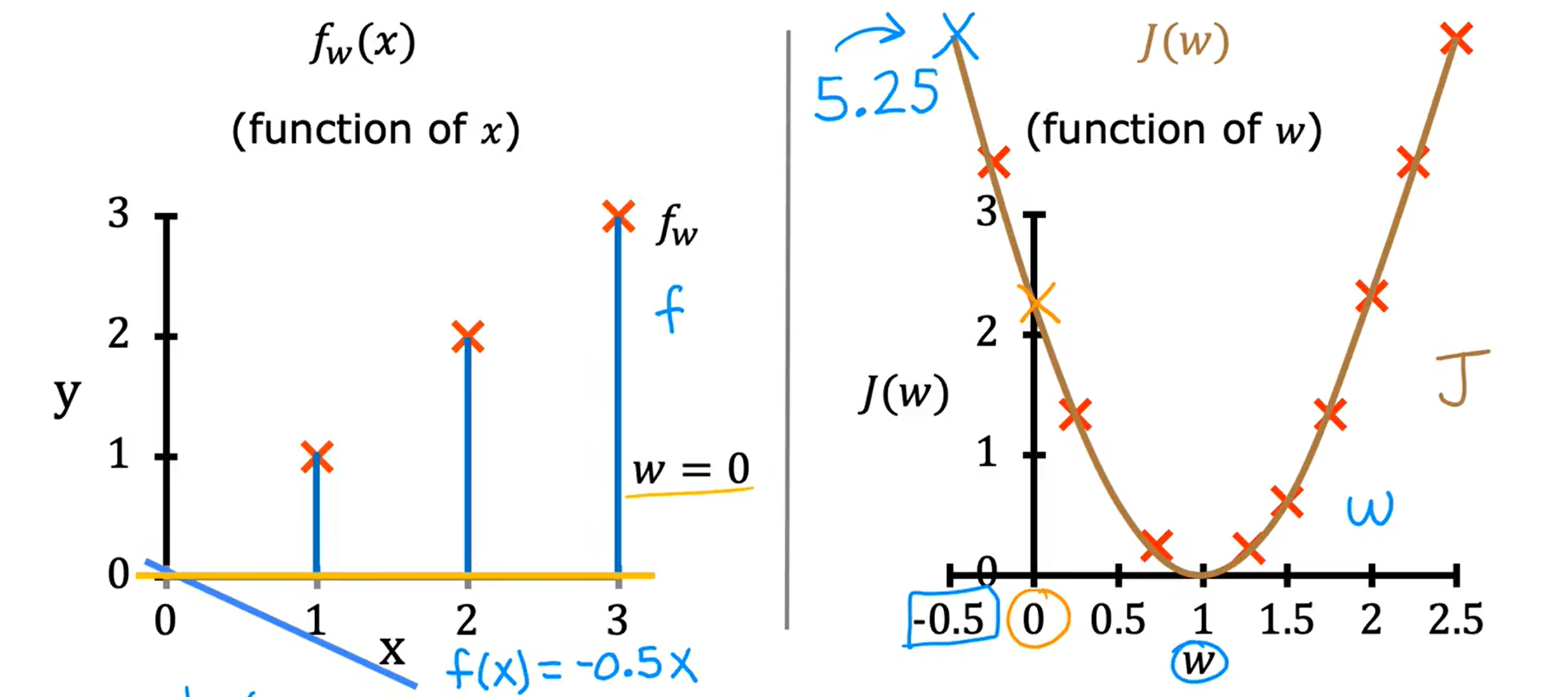 ### 可视化代价函数 代价函数 $J(w,b)$ 是一个三维曲面图,类似于一个汤碗或吊床的形状,表示不同参数 $w$ 和 $b$ 选择下的 $J$ 值。任何一个点都代表特定的 $J(w,b)$ 选择,点到曲面高度的距离是J值,同时,也可以使用等高线画出函数 $J(w,b)$。 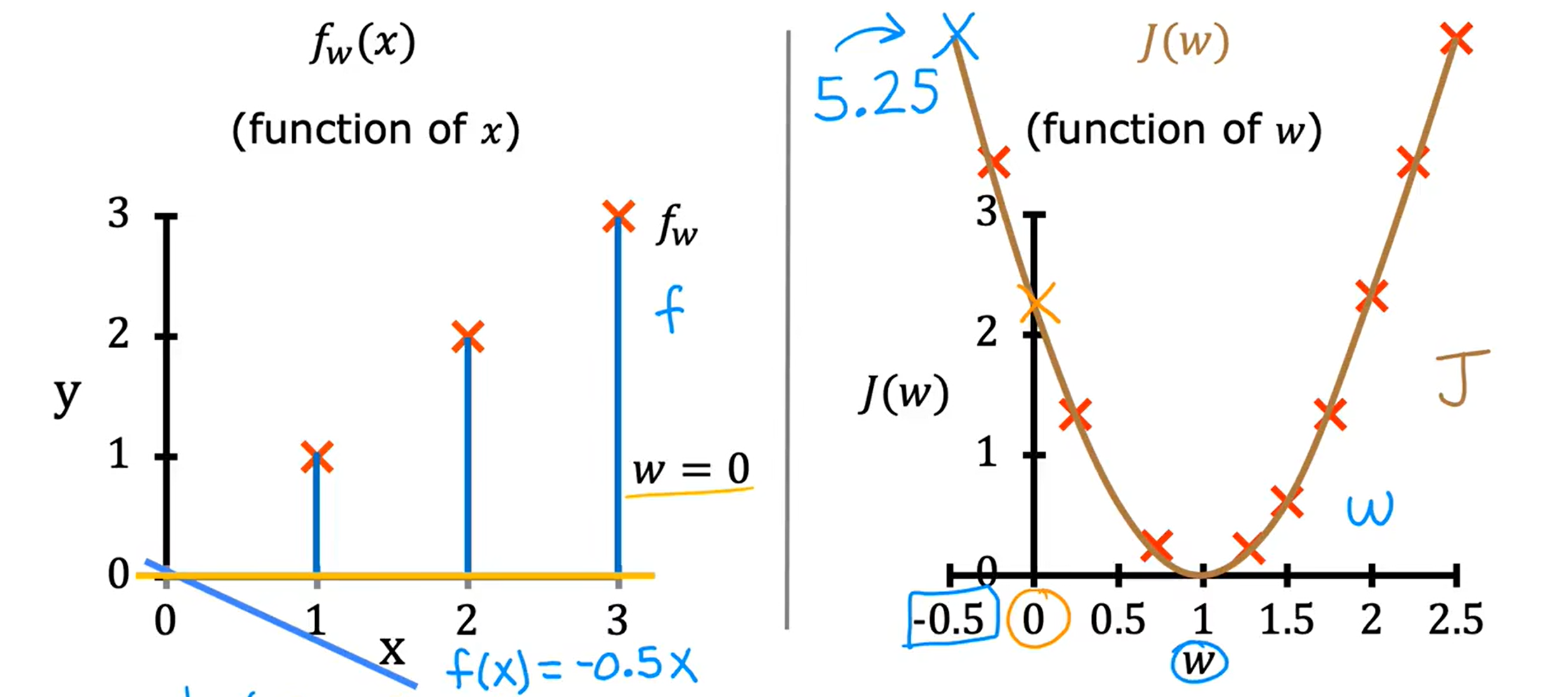 ## 2.3 梯度下降(Gradient Descent) 梯度下降是一种优化算法,可用于训练机器学习模型。梯度下降的目标是最小化成本函数,在本周的课程中,我们将学习如何使用梯度下降来训练线性回归模型,以便能够预测连续值输出。 ### 梯度下降(Gradient Descent) 梯度下降法是用来最小化任意函数的算法,其中代价函数 $J$ 是最小化的目标。在使用梯度下降法时,需要为权重参数 $w$ 和偏置参数 $b$ 猜测一些初始值,然后通过不断一点点改变权重参数 $w$ 和偏置参数 $b$ 以试图降低代价 $J$ 的值,直到 $J$ 在最小值或接近最小值。但需要注意的是,对于某些函数 $J$,梯度下降法可能找到的是局部最小值,而非全局最小值。 > 以下是一个非平方误差损失函数 & 非线性回归 的损失函数图像,选择不同的权重参数 $w$ 和偏置参数 $b$ 初始值,可能会梯度下降到不同的山谷中。 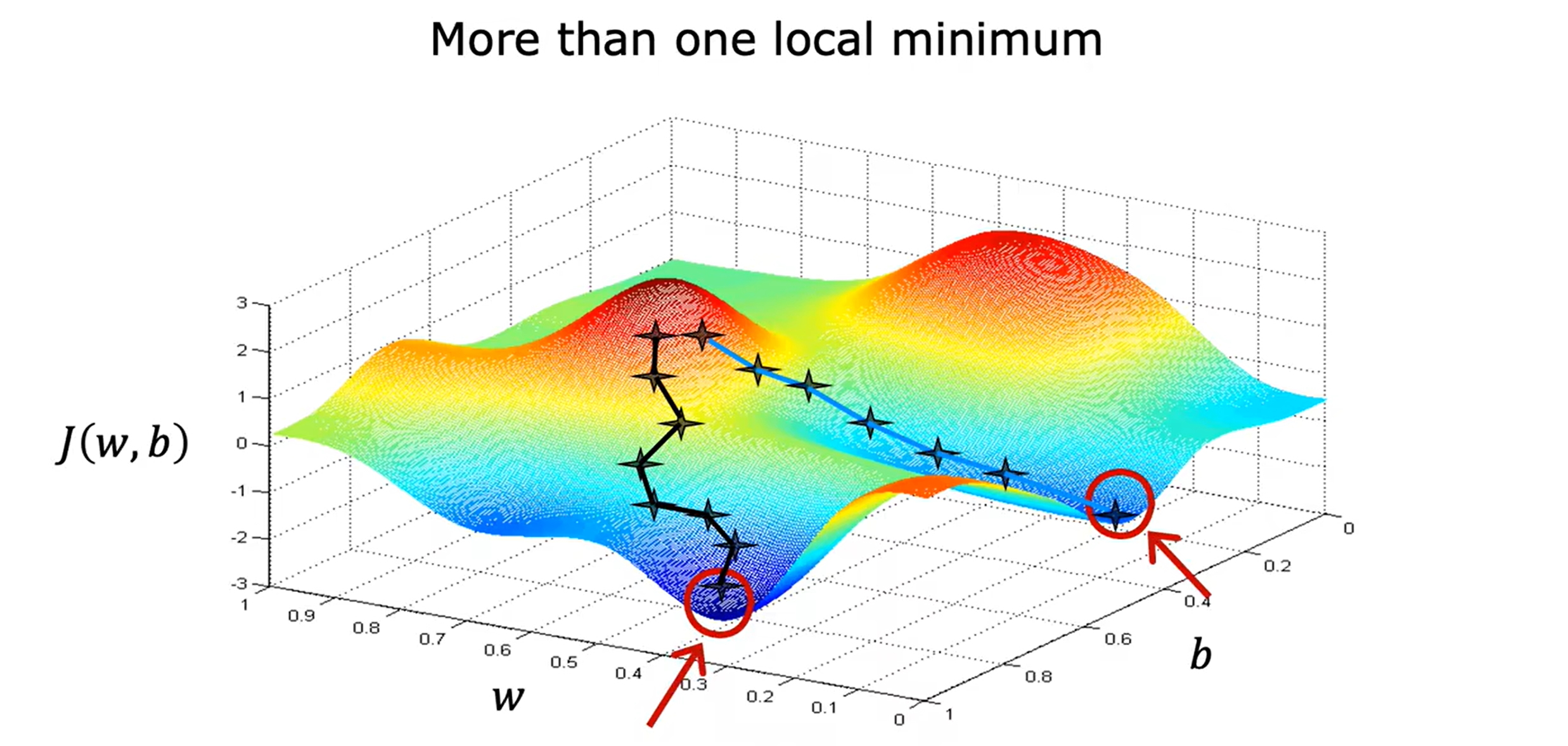 ### 梯度下降的实现 如下两个公式是梯度下降算法中用来更新权重参数 $w$ 和偏置参数 $b$ 的公式。其中,$J(w,b)$ 是损失函数,$w$ 和 $b$ 分别是权重参数和偏置参数,$\alpha$ 是学习率,$\frac{\partial J(w,b)}{\partial w}$ 和 $\frac{\partial J(w,b)}{\partial b}$ 分别是损失函数关于 $w$ 和 $b$ 的偏导数。  <div class="tip inlineBlock info simple"> 💡 Tip:此处的等号为赋值,并非断言。 </div> | | **代码赋值** | **数学断言** | | ------------ | ------------------------------------- | ---------------------------------- | | **定义** | 将一个值或表达式赋给一个变量 | 对某个数学命题的肯定或否定 | | **应用场景** | 计算机程序中,用来存储和处理数据 | 数学推理中,用来验证和证明数学命题 | | **表示方式** | 以赋值符号 "=" 将值或表达式与变量连接 | 以数学符号和逻辑符号表示 | | **例子** | a = 2; b = a + 3; | 对于任意实数 x,x^2 >= 0 | 在梯度下降算法中,我们希望通过不断地迭代更新权重参数和偏置参数,使得损失函数 $J(w,b)$ 在每一次迭代中都能够更接近最小值。具体地,每一次迭代中,我们可以使用公式 $w = w - \alpha\frac{\partial J(w,b)}{\partial w}$ 和 $b = b - \alpha\frac{\partial J(w,b)}{\partial b}$ 来分别更新权重参数和偏置参数的值。 <div class="tip inlineBlock info simple"> 💡 Tip:因为参数 $w$ 在后续更新参数 $b$ 时会被使用到,所以需要先存储在临时变量 tmp\_w 中,在完成 tmp\_b 后再将 tmp\_w 更新到参数 $w$,同时更新参数 $b$。 </div>  ### 理解梯度下降 在仅有一个参数 $w$ 的代价函数 $J(w)$ 中,梯度下降的更新公式为:$w = w - \alpha\frac{\partial J(w)}{\partial w}$,其中 $\alpha$ 是学习率,$\frac{\partial J(w)}{\partial w}$ 是代价函数 $J$ 在 $w$ 点处的导数。梯度下降算法的目标是让代价函数 $J$ 最小化,通过不断更新 $w$ 的值,使得 $J(w)$ 逐渐减小。在代价函数 $J(w)$ 的图像中,横轴是参数 $w$,纵轴是代价 $J(w)$,我们需要随着梯度下降使得 $w$ 值从初始化点开始,向代价函数 $J(w)$ 减小的方向移动。 梯度下降的工作原理是基于代价函数在当前点的导数,代价函数在该点的斜率越陡峭(导数越大),梯度下降的更新步长也就越大,以便更快地到达最小值。当斜率为正时,表示代价函数 $J$ 在该点处上升,梯度下降会将 $w$ 向左移动,以减小 $J(w)$ 的值,逐渐接近 $J(w)$ 的最小值,当斜率为负时,则正好相反。 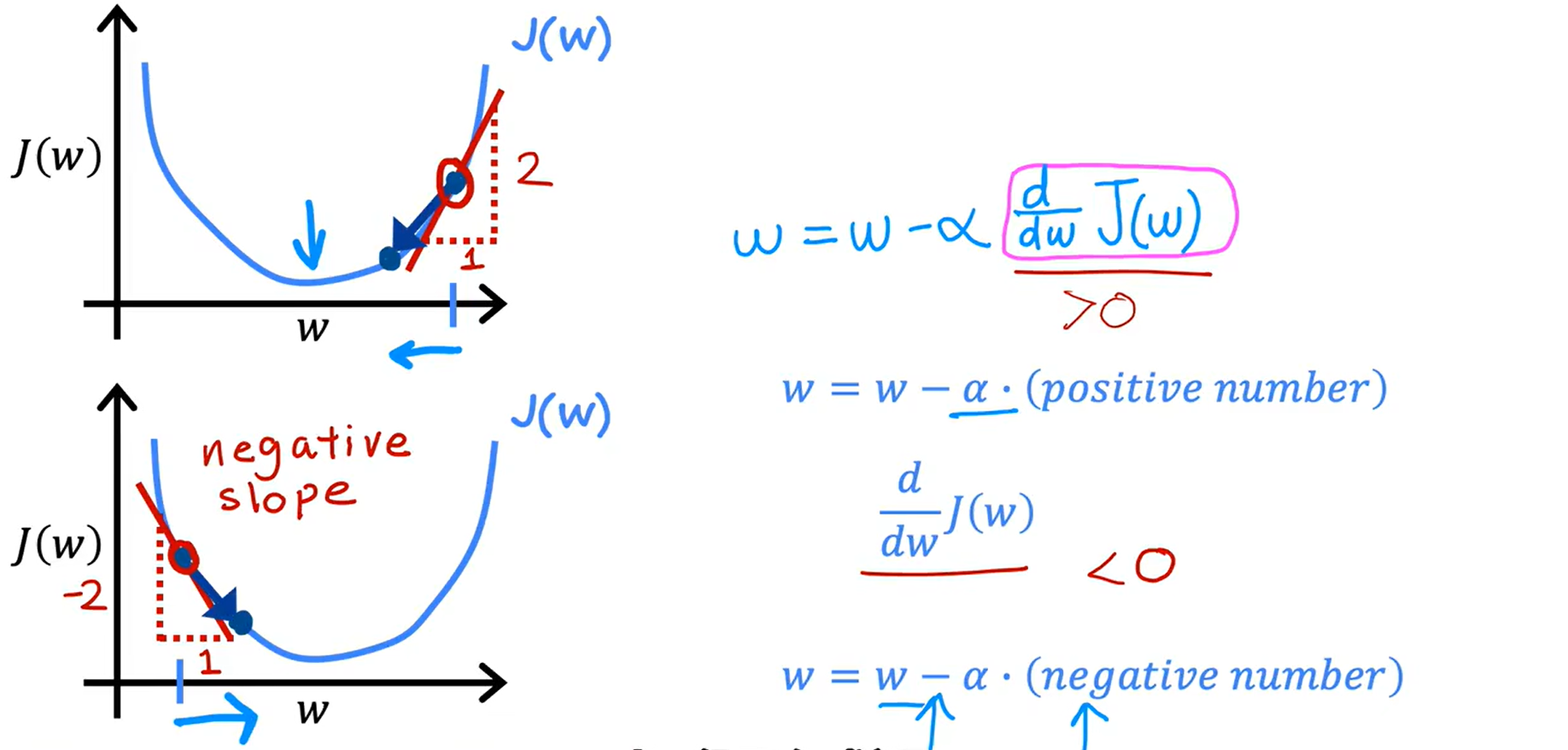 ## 2.4 学习率(Learning Rate) 在梯度下降中,学习率是一个非常重要的参数,它控制了参数更新过程中的步长大小。如果学习率设置得过小,优化过程会非常缓慢,可能需要很长时间才能收敛到最优解;而如果学习率设置得过大,会导致更新步长过大,可能会错过最优解并发散。因此,选择合适的学习率是非常重要的,需要根据具体情况进行调整。 * 学习率过小,从图中我们可以发现,随着 $w$ 不断接近 $J(w)$ 的最小值点,$w$ 更新的步长也会不断减小,直到最终达到最小值点。  * 学习率过大,同上图一样可以看出,由于越过了最小值点,所以斜率(该点导数)可能会恰巧增大导致 $w$ 更新步长的增加,从而无法收敛。  如果参数已经达到局部最小值,进一步的梯度下降步骤将不会有任何作用,因为此时梯度为零,参数已经无法再更新了。这也解释了为什么梯度下降可以达到局部最小值,即使使用固定的学习率,梯度下降也可以通过不断迭代来逐渐接近最小值。但需要注意的是,梯度下降可能会陷入局部最小值,而无法达到全局最小值,因此需要使用一些优化算法来避免这种情况。 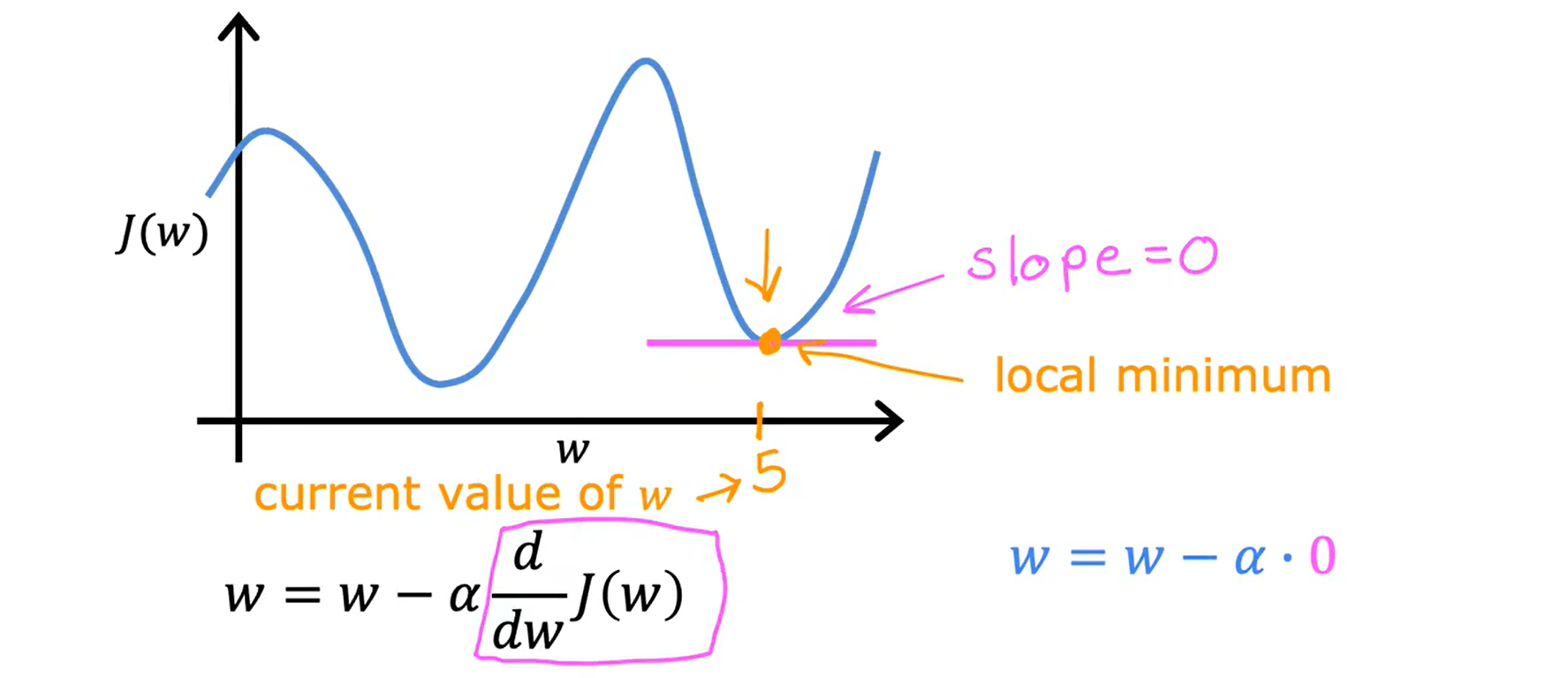 ## 2.5 用于线性回归的梯度下降 根据我们已有的线性回归模型及其平方误差损失函数,为了使用梯度下降算法来实现线性回归模型的拟合过程,需要对平方误差损失函数进行求导。在求导时,根据微积分相关知识,平方求导后会存在一个乘数 2,而平方误差损失函数中的 2 可以被消去。为了简化计算,通常会将平方误差损失函数除以 2m,这样在求导后的结果中也可以消去分母中的 2。 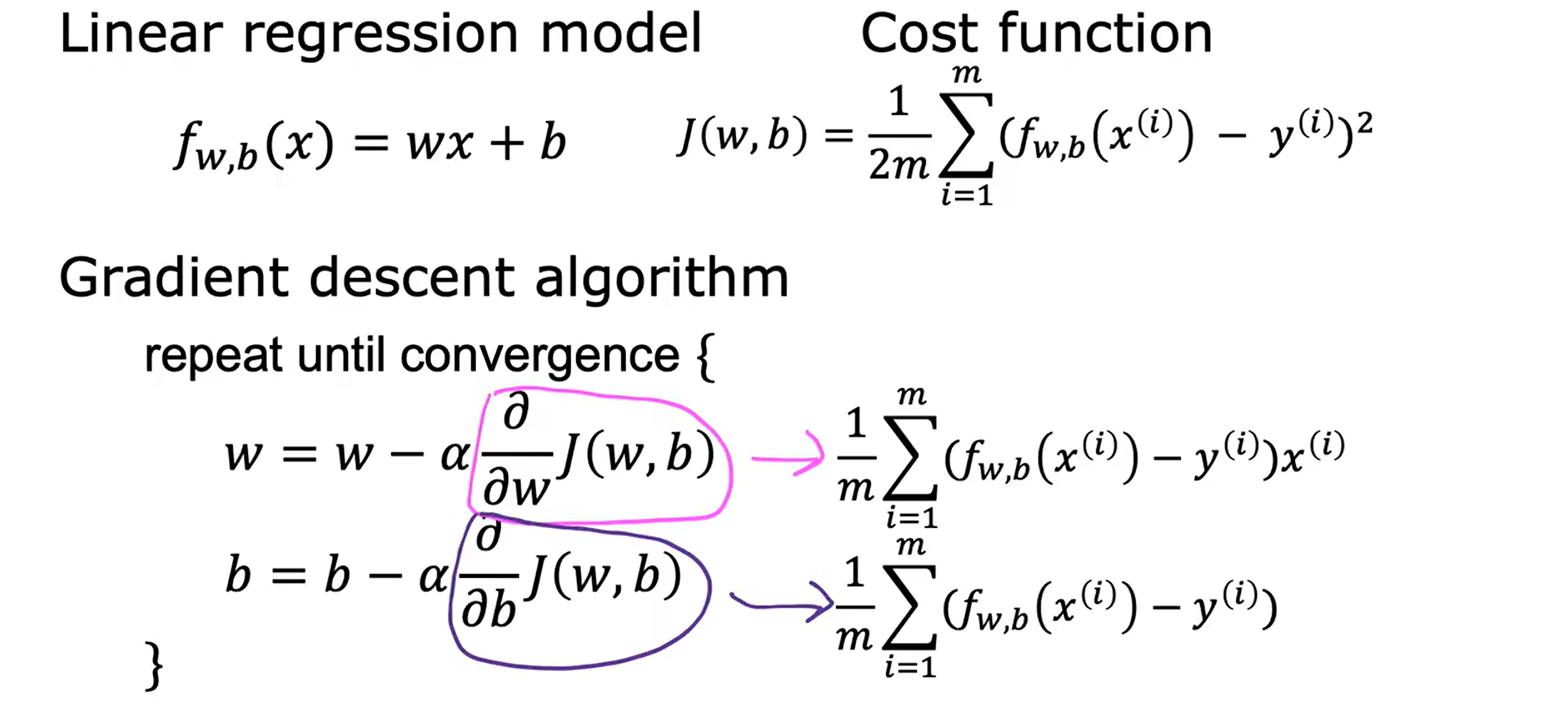 当使用误差平方代价函数进行线性回归时,该代价函数是一个凸函数,具有以下特点: * 代价函数是一个碗状的函数,只有一个最小值点; * 除了单一的全局最小值以外,不可能有任何局部最小值。 因此,使用梯度下降算法时,只要选择合适的学习率,就能保证算法收敛于全局最小值,从而得到最优的参数解。 凸函数在优化问题中具有重要作用,因为它们可以保证最优解的唯一性和全局最优性。除了线性回归中的误差平方代价函数,还有一些其他函数也是凸函数,如正则化代价函数中的L1和L2正则化项。  ## 2.6 可视化展示 ### 梯度下降迭代展示 如图所示代价函数在模型参数空间中的可视化,并演示了梯度下降算法在此空间中的迭代过程,包含以下要点: * 左上角为数据和模型图表,右上角用等高线图表示代价函数在参数空间中的分布,底部为对应代价函数的曲面图; * 参数 $w$ 和 $b$ 通常会被初始化为 0,但在此演示中初始化为 $w=-1$ 和 $b=1$,对应的模型函数为 $f(x)=-x+1$; * 利用梯度下降法更新参数 $w$ 和 $b$,每次迭代会使代价函数沿着梯度方向下降一定程度,随着迭代次数的增加,代价函数不断下降,参数 $w$ 和 $b$ 沿着曲面的轨迹进行更新; * 最终达到全局最小值,对应于使代价函数最小化的最优参数 $w$ 和 $b$,此时拟合的直线最好地拟合了数据。  ### 批量梯度下降(Batch Gradient Descent) 批量梯度下降是梯度下降算法的一种,每次梯度下降时都会考虑到所有的训练样本,而不是训练数据的子集。因此,在计算梯度下降时,需要计算所有训练样本的导数之和,正如我们在上述线性回归模型梯度下降所展示的那样。虽然还有其他梯度下降算法不会使用整个数据集,而是在每个更新步骤中使用小的训练数据子集,但批量梯度下降仍然是应用广泛的算法之一。 # 3、多元线性回归 ## 3.1 多维特征(Multiple Features) 相比于单变量线性回归,多元线性回归使用了多个特征来预测目标变量,**多维特征**指的是在多元线性回归中使用的特征或属性,也可以称为自变量或输入变量。例如,当预测房价时,使用的特征可能包括房屋面积、卧室数量、厨房数量等等。 ### 术语表示 下图为关于多变量线性回归中使用的符号表示的说明。其中,X 表示特征矩阵,包含了所有的训练样本以及每个样本的特征值。 * $x_j$ 表示特征列表中的第 j 个特征。 * 小写字母 n 表示特征的总数。 * $\vec{x}^{(i)}$ 表示第 i 个训练样本的特征向量,是由四个数字组成的列表。 * 为了引用第 i 个训练样本中的一个特定特征,可以使用 ${x}^{(i)}_j$ 表示。  ### 多元线性回归模型 我们之前定义了一个只有单特征的模型,现在我们需要用不同的方式来定义一个多特征的模型。我们的模型包含四个特征,由参数 $w_1$、$w_2$、$w_3$、$w_4$ 和偏移量 $b$ 组成。举个例子,我们可以用这个模型来预测房价。  针对具有 n 个特征的多元线性回归模型,我们可以通过引入符号来简化模型表达式。定义 $\vec{w}$ 为包含参数 $w_1$ 至 $w_n$ 的数字列表,用小箭头表示其为一个向量。同样地,用 $\vec{x}$ 为包含特征 $x_1$ 至 $x_n$ 的数字列表。这样,我们可以将模型表示为 $f(x)=\vec{w}·\vec{x} + b$,其中 $\vec{w}·\vec{x}$ 是 $w$ 和 $x$ 的点积,即 $w_1 * x_1 + w_2 * x_2 + w_3 * x_3 + ......+ w_n * x_n$,最后再加上常数项 $b$。 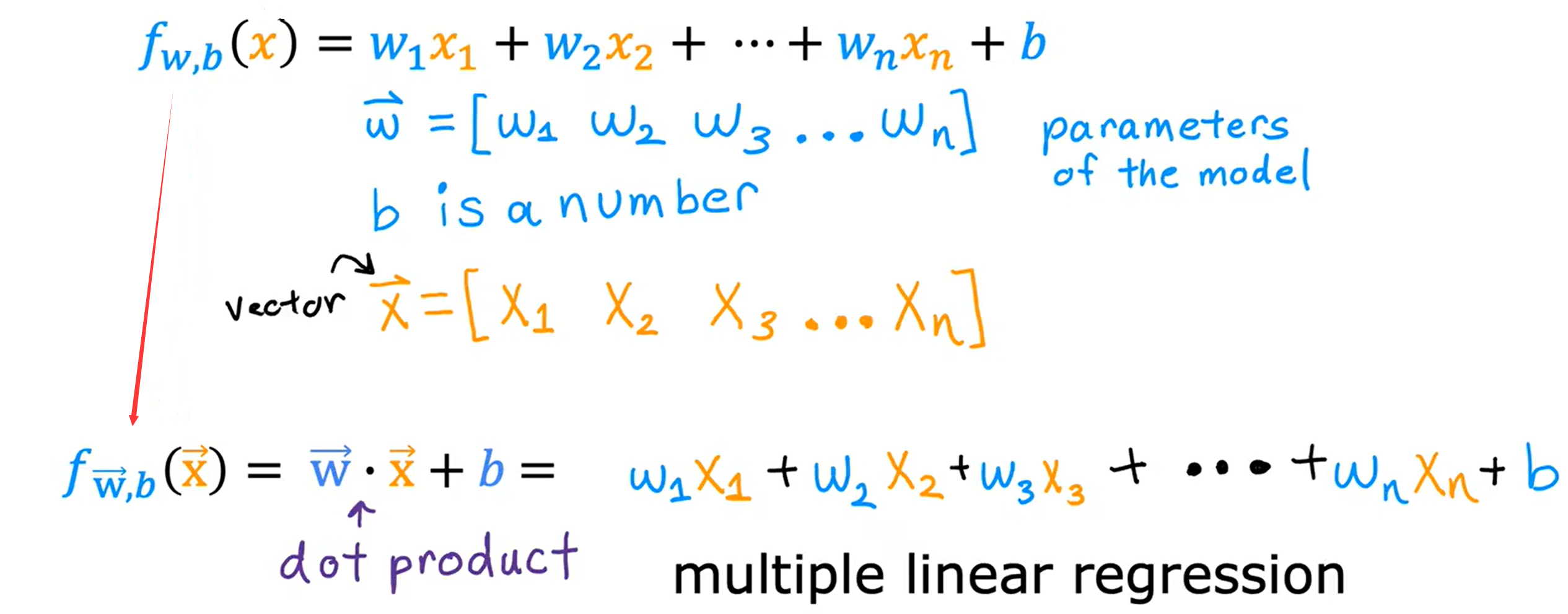 ## 3.2 矢量化(Vectorization) 向量化可以减少代码量,提高运行效率,是机器学习算法中常用的优化方法。在使用时,可以利用现代数值线性代数函数库和计算机的GPU硬件来加速计算,进一步提高效率。 向量化的具体例子:假设有一个一个多特征的模型。我们的模型包含四个特征 $x_1$、$x_2$、$x_3$、$x_4$,以及参数 $w_1$、$w_2$、$w_3$、$w_4$ 和偏移量 $b$ 组成。所以 n 等于 4,我们可以使用数组来定义这些变量 $w$、$b$ 和 $x$,例如: ```python import numpy as np w = np.array([1, 2, 3, 4]) b = 8 x = np.array([5, 6, 7, 8]) ``` <div class="tip inlineBlock info simple"> 💡 此处使用 NumPy 库,NumPy 是用于科学计算和数据分析的 Python 库,支持大量的数学运算,包括线性代数、傅里叶变换、随机数生成等,是Python中最常用的数学库之一。 </div> 1. **非矢量化表示:手动枚举计算** ```python f = w[0] * x[0] + w[1] * x[1] + w[2] * x[2] + w[3] * x[3] + b ``` 2. **非矢量化表示:自动循环计算** ```python f = 0 for j in range(4): f += w[j] * x[j] f += b ``` 3. **矢量化表示:向量点乘计算** ```python f = np.dot(w, x) + b ``` 简单来说,向量化可以简化代码,提高可读性,同时也可以显著提高代码的运行速度。 在下图中,左边代码使用了 for 循环来计算向量乘法的结果,当 j 的取值范围是 0 到 15 时,该代码一个接一个地执行操作。与之相反,右边代码使用 NumPy 中的 dot 函数通过计算机硬件实现向量化。计算机可以得到向量 $\vec{w}$ 和 $\vec{x}$ 的所有值,然后同时并行地将向量 $\vec{w}$ 和 $\vec{x}$ 相乘,通过计算机调用专门的硬件,非常高效地计算这 16 个数字的和。 这意味着,使用向量化的代码跑起来会快很多,当在大型数据集上运行算法或训练大模型时,这点尤其重要。所以向量化是高效运行算法的关键步骤,还可以很好地扩展到许多运行在大型数据集的现代机器学习算法上。 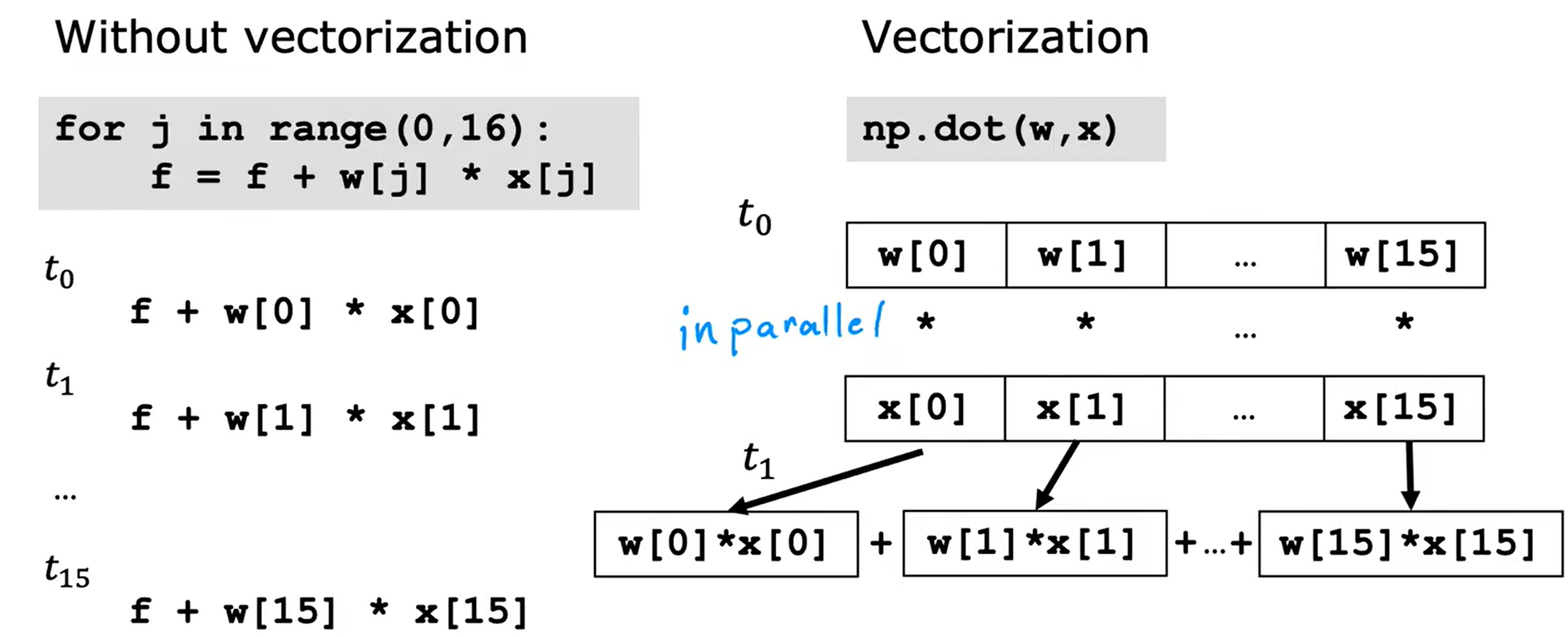  ## 3.3 多元线性回归的梯度下降 ### 多元线性回归的梯度下降 简单回顾多元线性回归模型及其梯度下降的向量表示。  当样本具有多个特征时,我们需要使用多元线性回归模型来拟合数据,与单变量回归不同的是,多元回归中我们有多个特征,需要对每个特征的参数进行更新。需要注意的是,每个 $w_j$ 更新时,学习率 $\alpha$ 所乘的导数为 $J(\vec{w},b)$ 对 $w_j$ 的偏导数: $$ w_j = w_j - \alpha\frac{1}{m}\sum_{i=1}^{m}(f_{\vec{w},b}(x^{(i)})-y^{(i)})x_j^{(i)} $$  ### 正规方程(Normal Equation) 在线性回归中,梯度下降法是一种常用的方法,用于最小化代价函数 $J$,以找到 $w$ 和 $b$。然而,在线性回归中还有另一种求解 $w$ 和 $b$ 的方法,称为正规方程法。大多数机器学习从业者无需自己实现正规方程法,因为现有的机器学习库可以在后台调用这种方法来求解 $w$ 和 $b$。【[详解正规方程](https://zhuanlan.zhihu.com/p/60719445)】 相较于梯度下降其优缺点如下: * **√ 无需迭代即可计算 $w$ 和 $b$** * **× 无法推广到其他学习算法,只能用于线性回归** * **× 如果特征数据量很大的话,计算会变得非常慢** # 4、实用线性回归技巧 ## 4.1 特征缩放(Feature Scaling) 在使用梯度下降算法时,特征缩放可以提高算法的收敛速度。这是因为如果不进行特征缩放,则特征值范围较大的特征将对代价函数的梯度产生更大的影响,从而导致算法收敛速度慢。 ### 特征大小和梯度下降 当特征的值域差异很大时,例如在房价预测问题中,房子的大小可能是300到2000平方英尺,而卧室数量可能在0到5之间,不同参数 如果不进行特征缩放,代价函数的等高线图会呈现出高度狭长的形态,使得梯度下降在找到全局最小值之前可能会反复横跳。 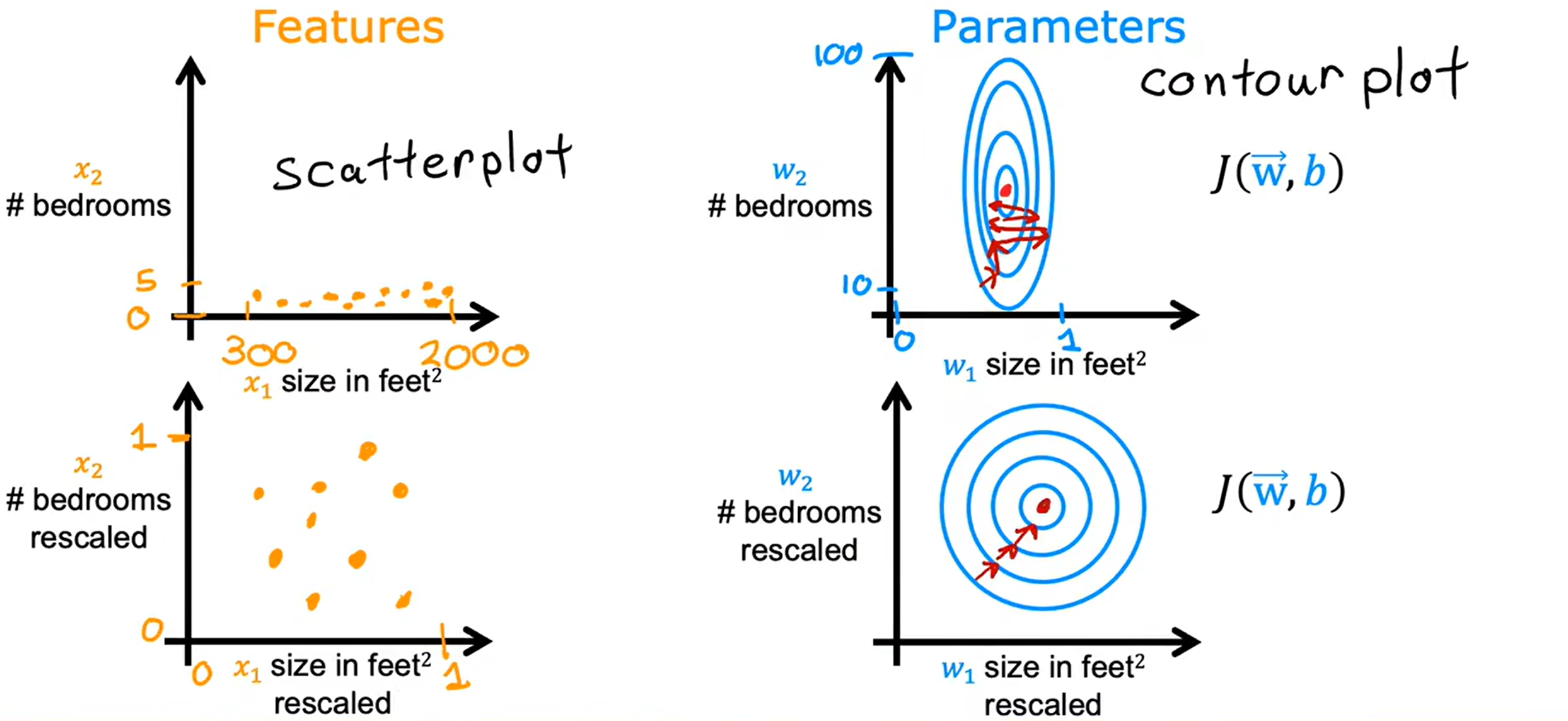 ### 归一化缩放(Min-Max Scaling) 将每个特征的值缩放至一个固定的范围,通常是 [0,1]。对于每个特征,计算它的最小值和最大值,然后使用以下公式分别将该特征缩放至 [0,1] 范围内: $$ x_{scaled} = \frac{x_{original} - min}{max - min} $$ 下图的缩放方式为直接除以最大值进行缩放,即 $x_{scaled} = \frac{x_{original}}{max}$。  ### 均值归一化(Mean Normalization) 均值归一化是通过原始数据中的均值、最大值和最小值来进行数据标准化,。对于每个特征,计算它的最小值、最大值以及样本均值 $\mu$,然后使用以下公式分别将该特征缩放至 [-1,1] 范围内: $$ x_{scaled} = \frac{x_{original} - \mu}{max - min} $$  ### Z-Score 标准化(Z-Score Normalization) Z-Score 标准化可以将每个特征的值缩放至其均值为 0,标准差为 1 的分布上。对于每个特征,计算它的均值和标准差,然后使用以下公式将该特征进行标准化: $$ x_{scaled} = \frac{x_{original} - \mu}{\sigma} $$ 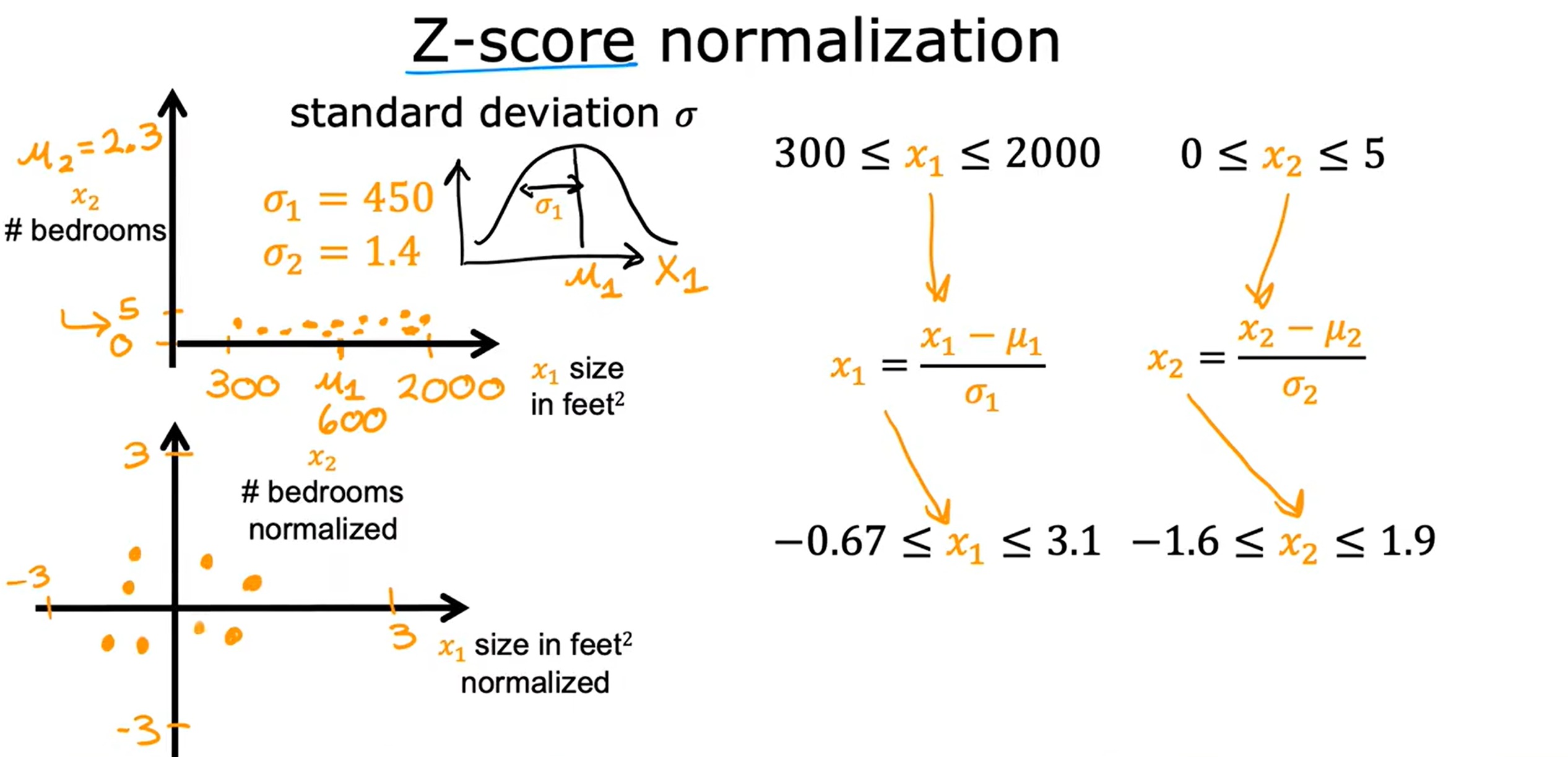 ### 是否需要特征缩放 一般来说,将每个特征的取值范围定在-1到1附近是比较好的,但在某些情况下,特征的取值范围可能会比较宽松,这时可以考虑将其放缩到合适的范围内。特征放缩可以使梯度下降跑得更快,而且几乎没有什么害处。  ## 4.2 检查梯度下降的收敛性 绘制学习曲线(代价函数-迭代次数图像)有助于你了解每次梯度下降迭代后成本J的变化情况。如果梯度下降正常运作,那么每次迭代后代价 $J$ 应该会降低。如果代价 $J$ 的值在一次迭代后反而增加了,这意味着要么学习率 $\alpha$ 选择得不好,通常意味着 $\alpha$ 太大,或者代码中存在 bug。 另一种判断什么时候完成模型训练的方法是使用自动收敛测试,我们用希腊字母 $\epsilon$ 表示一个小数字的变量,如 0.001,即 $10^{-3}$。如果代价 $J$ 在一次迭代中减少的量小于这个数,那么可以说它收敛了,但是选出合适正确的 $\epsilon$ 是相当困难的。  ## 4.3 选择学习率 学习率对于梯度下降算法的性能起着至关重要的作用,如果学习率选择得当,算法可以很好地运行。如果学习率太小,算法可能运行得太慢,而如果学习率太大,则可能无法收敛。如果代价在每次迭代后增加,可能是学习率太大或代码有 bug 导致的,可以通过选择较小的学习率和检查代码来解决,同时,我们可以绘制代价-迭代次数图,来选择合适的学习率。  当使用梯度下降法时,可以从一个较小的学习率值开始,然后将每次尝试的 $\alpha$ 值选取为前一个值的大约 3 倍,直到找到一个合适的 $\alpha$ 值,确保代价不会下降太慢,同时使代价函数 $J$ 不会反复横跳。对于每个不同的 $\alpha$ 值,可以用梯度下降法进行少量的迭代,并绘制代价函数 $J$ 与迭代次数之间的关系图像(学习曲线)。   ## 4.4 特征工程(Feature Engineering) 特征工程是指对原始数据进行处理和转换,以创建新的特征来提高机器学习算法的性能和准确性。在特征工程中,可以运用专业知识或直觉来设计新的特征,这些特征能够更好地预测目标变量,使机器学习算法更容易做出准确的预测。 假设每个房子有两个特征:房屋所在地块的宽度 $x_1$ 和长度 $x_2$。通过这两个特征,可以建立一个模型 $f(x) = w_1 * x_1 + w_2 * x_2 + b$ 来预测房价。但是,土地面积 $x_3 = x_1 * x_2$ 可能比宽度和长度特征更能预测价格。因此,我们可以定义一个新特征 $x_3$,将其等于土地面积。通过这个新特征,可以建立一个新模型 $f_{w, b}(x) = w_1 * x_1 + w_2 * x_2 + w_3 * x_3 + b$,其中特征 $x_3$ 是预测房价的最重要因素。 ## 4.5 多项式回归(Polynomial Regression) 多项式回归是一种线性回归的扩展形式,通过将输入特征的高次幂引入模型,可以拟合更复杂的非线性关系。特征幂次的选择需要结合数据集实际情况,以求得最优的拟合效果,例如下图三种模型都可以拟合当前数据。需要注意的是,当特征为原始特征的幂时,特征放缩非常重要,因为不同特征的取值范围可能相差非常大。 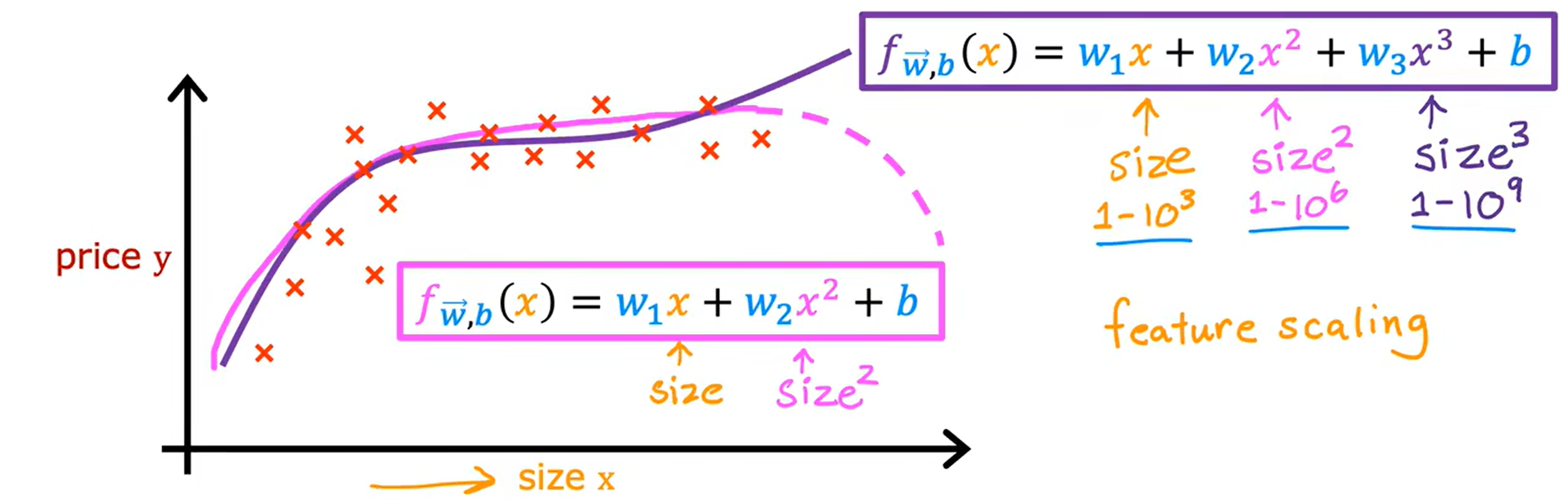 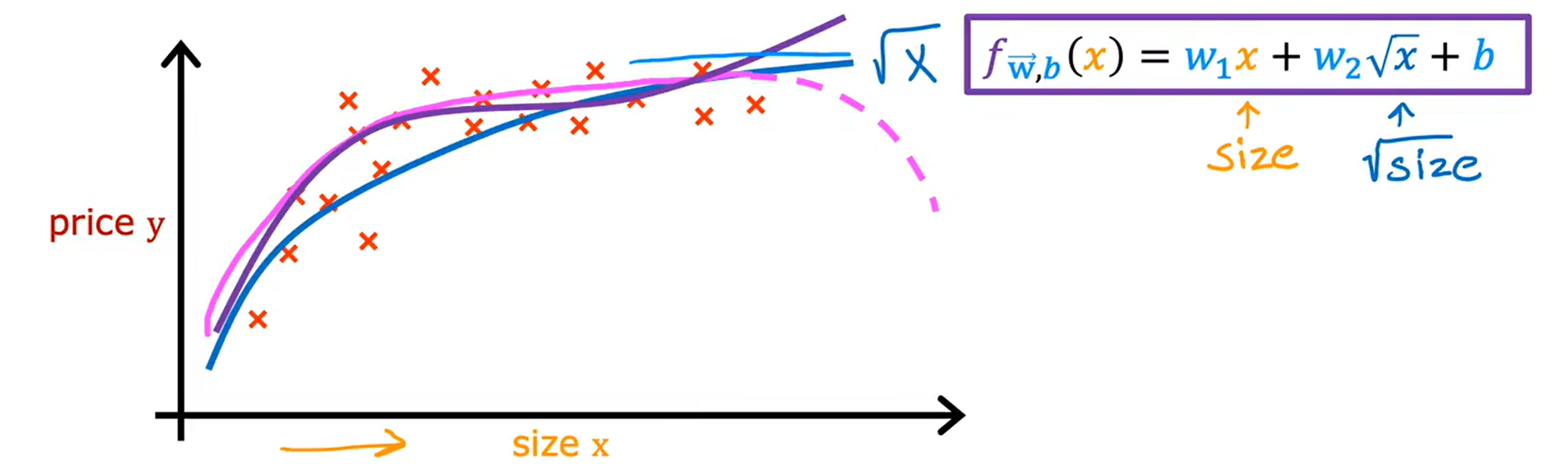 # 5、逻辑回归 ## 5.1 原因 & 动机(Motivation) ### 二元分类(Binary Classification) 当我们需要预测的变量只有两种可能值时,例如判断是否是垃圾邮件、判断肿瘤是恶性还是良性,我们通常会用“否”或“是”、“假”或“真”、“0”或“1”等表示两个类别。正样本和负样本也是常见的术语,用来表示是否存在某种情况,正负样本并不代表样本的好坏,只是为了传达 “**presence/true/one**” 或者 “**absence/false/zero**” 的概念。  ### 线性回归拟合分类问题 在使用线性回归时,我们可以选择一个阈值(比如0.5)来将预测值转换为类别。取阈值等于 0.5 的点,预测值在该点左边的所有数据点都被预测为 0 类(肿瘤不是恶性的),右边的所有数据点都被预测为 1 类(肿瘤是恶性的)。但是,当在数据集中添加一个新的数据点时,最佳拟合线就会右移,导致原本被正确分类的数据点变为错误分类,所以线性回归算法可能不适用于分类问题。 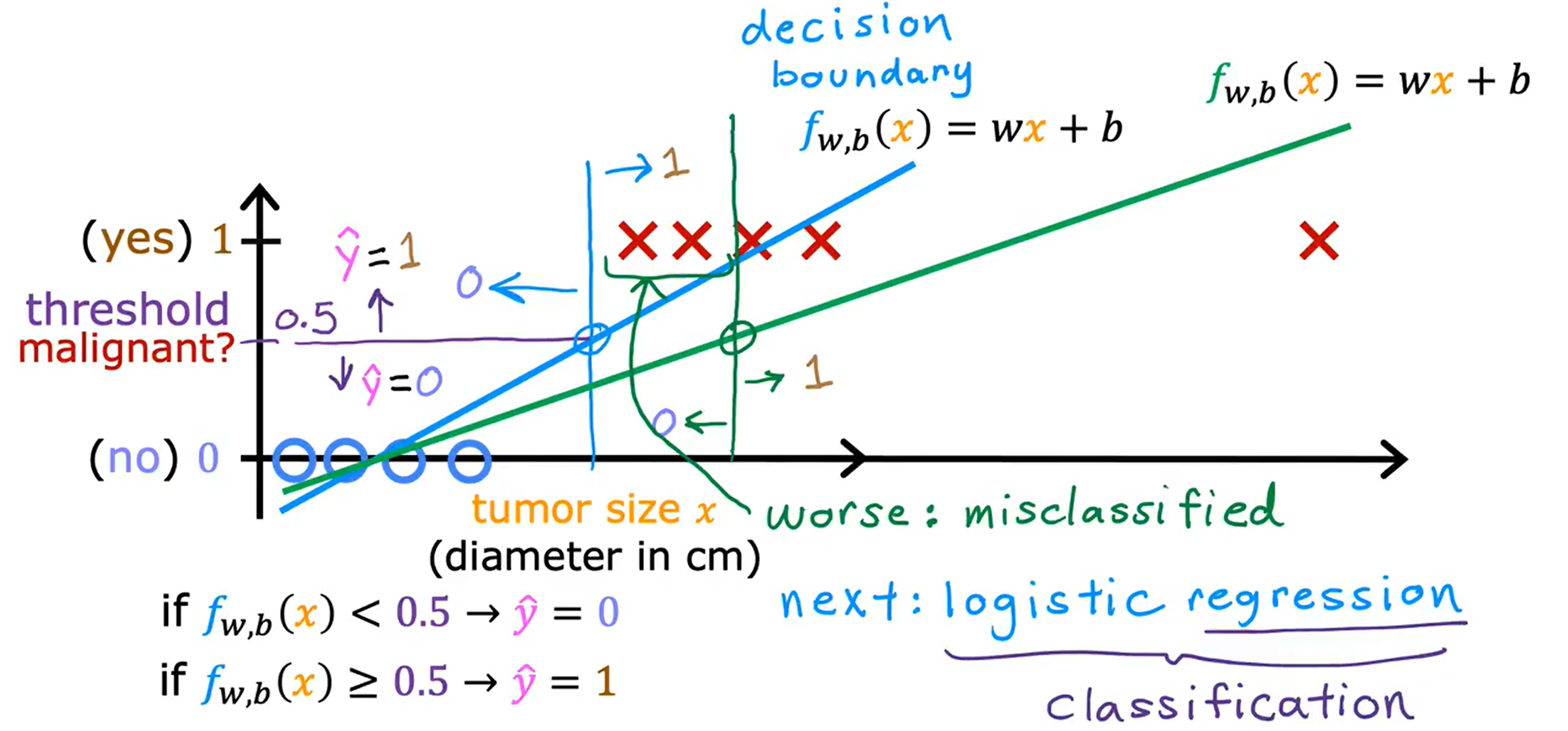 ## 5.2 逻辑回归(Logistic Regression) ### Sigmoid 函数 逻辑回归算法需要用到 Sigmoid 函数,它是一种重要的数学函数,也叫做逻辑函数。Sigmoid 函数的输出值在 0 到 1 之间,可用公式 $g(z) = \frac{1}{1 + e^{-z}}$ 来表示,其中 $e$ 是数学常数,取值约为 2.71,$z$ 为函数的自变量。 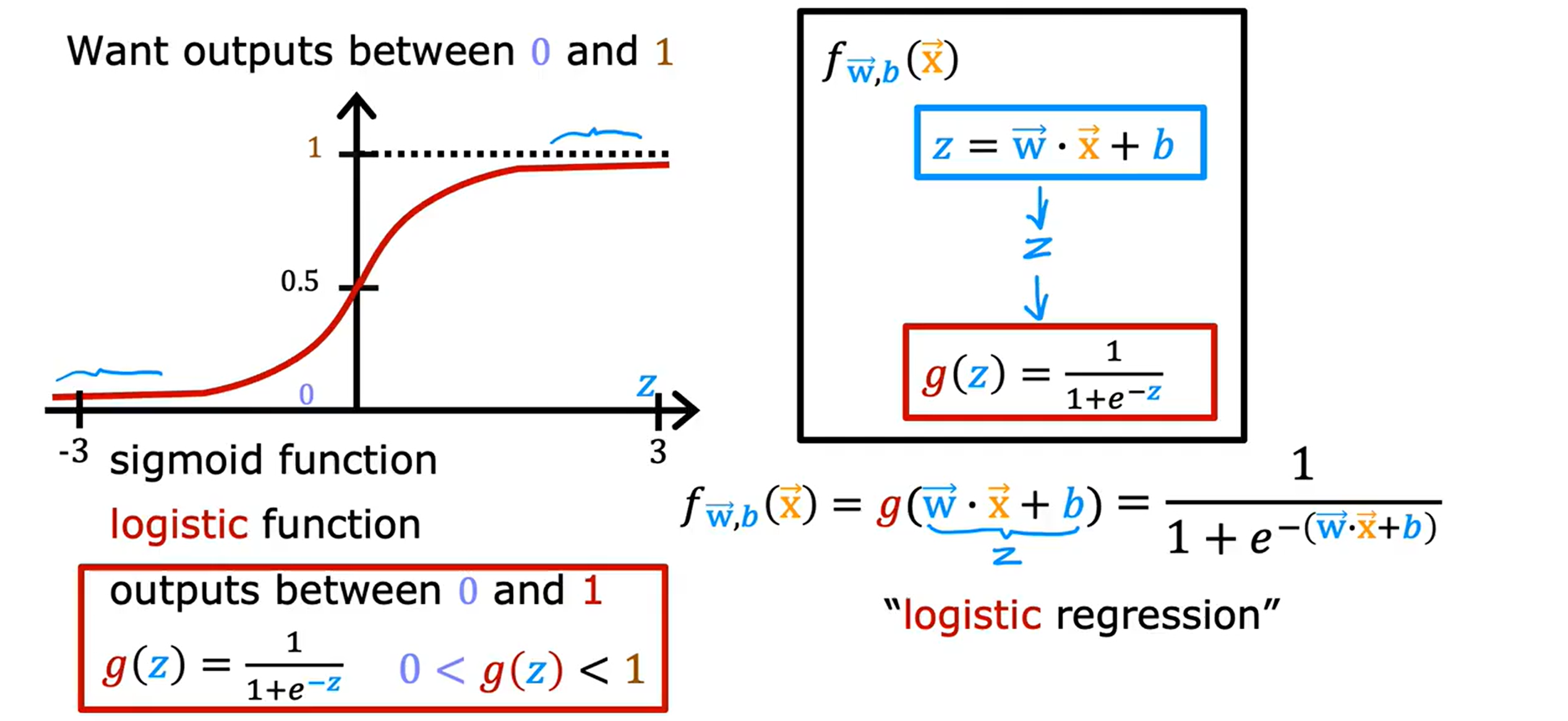 ### 逻辑回归模型 我们可以根据 Sigmoid 函数来建立逻辑回归算法,我们需要计算 $z$ 值,即线性回归函数 $F_{\vec{w},b}(\vec{x}) = \vec{w}·\vec{x}+b$,我们将其赋值给变量 $z$。然后,将 $z$ 值传递给 Sigmoid 函数,即逻辑函数 $g(z) = \frac{1}{1 + e^{-z}}$,其结果在 0 和 1 之间。整理上述过程得到逻辑回归模型: $$ F_{\vec{w},b}(\vec{x}) = \frac{1}{1 + e^{-(\vec{w}·\vec{x}+b)}} $$ 我们可以把其输出看作是在给定输入 x 的情况下,类别或标签 y 等于 1 的概率。例如,在本例中,x 为肿瘤大小,y 为 0 或 1,如果病人的肿瘤大小是 x,得到对应模型输出的是 0.7,这意味着模型预测有 70% 的概率这个病人的肿瘤是恶性的(即 y 等于 1)。  ## 5.3 决策边界(Decision Boundary) ### 选择阈值 如果想让算法预测 $\hat{y}$ 的值是 0 还是 1,我们可以设置一个阈值来预测。我们常常使用 0.5 作为阈值,当 $f_{\vec{w},b}(\vec{x})$ 大于或等于 0.5(即 $z = \vec{w} · \vec{x} + b$ 的值大于或等于0)时,则预测 $\hat{y}$ 是 1,否则预测 $y$ 是 0。其中,我们通常使用 $\hat{y}$ 来表示预测值。  ### 线性决策边界(Linear Decision Boundary) 在这个例子中,假设决策边界是 $x_1 + x_2 = 3$ 的一条直线,它将空间分成了左下方和右上方两个部分。当特征 $x$ 在决策边界的右侧时,逻辑回归模型将预测 $\hat{y}$ 为 1;当特征 $x$ 在决策边界的左侧时,模型将预测 $\hat{y}$ 为 0,这就是逻辑回归模型如何进行预测的基本原理。当参数的值不同时,决策边界也会不同,所以逻辑回归模型的表现和预测能力取决于参数的选择。  ### 非线性决策边界(Non-linear Decision Boundaries) 为了实现下图所示的圆形决策边界,我们定义 $z = w_1 * x_1^2 + w_2 * x_2^2 + b$,然后使用 $g(z)$ 对 $f_{\vec{w},b}(\vec{x})$ 进行预测。假设 $z = x_1^2 + x_2^2 - 1 = 0$,即决策边界为 $x_1^2 + x_2^2 = 1$,这意味着决策边界是一个圆形,它将空间分成了圆内和圆外两个部分。当 $x \geq 0$ 时,即处于圆形外的区域将被模型将预测 $\hat{y}$ 为 1,反之,预测 $\hat{y}$ 为 0。我们也可以使用多项式的不同组合来创建更复杂的决策边界。  ## 5.4 代价函数 ### 平方误差损失函数 ~ 存在问题 平方误差代价函数并不是逻辑回归的理想代价函数,逻辑回归的标签 y 只有两个值 0 或 1。逻辑回归的成本函数不同于线性回归,因为在逻辑回归的输出经过 Sigmoid 函数后,产生了非线性的形式,所以使用平方误差代价函数得到的逻辑回归的成本函数是非凸的。这意味着代价函数具有多个局部极小值,并且梯度下降算法可能会陷入其中一个局部极小值而无法达到全局最小值,不适合使用梯度下降法进行优化。  ### 逻辑损失函数(Logistic Loss Function) $$ f(x) = \begin{cases} - log(f_{\vec{w},b}(\vec{x}^{(i)})), & \text{ if } y^{(i)} = 1 \\ -log(1-f_{\vec{w},b}(\vec{x}^{(i)})), & \text{ if } y^{(i)} = 0 \end{cases} $$ 逻辑损失函数是用于逻辑回归模型的一种常用损失函数,用于衡量模型在一个样本上的表现。当样本真实标签为 1 时,损失函数为 $-log(f_{\vec{w},b}(\vec{x}^{(i)}))$,当样本真实标签为 0 时,损失函数为 $-log(1-f_{\vec{w},b}(\vec{x}^{(i)}))$。在样本真实标签为 1 时,损失函数会鼓励算法做出更准确的预测,使得损失最小,所以预测结果 $\hat{y}$ 越接近 1 损失越小,越接近 0 损失越大,反之亦然。 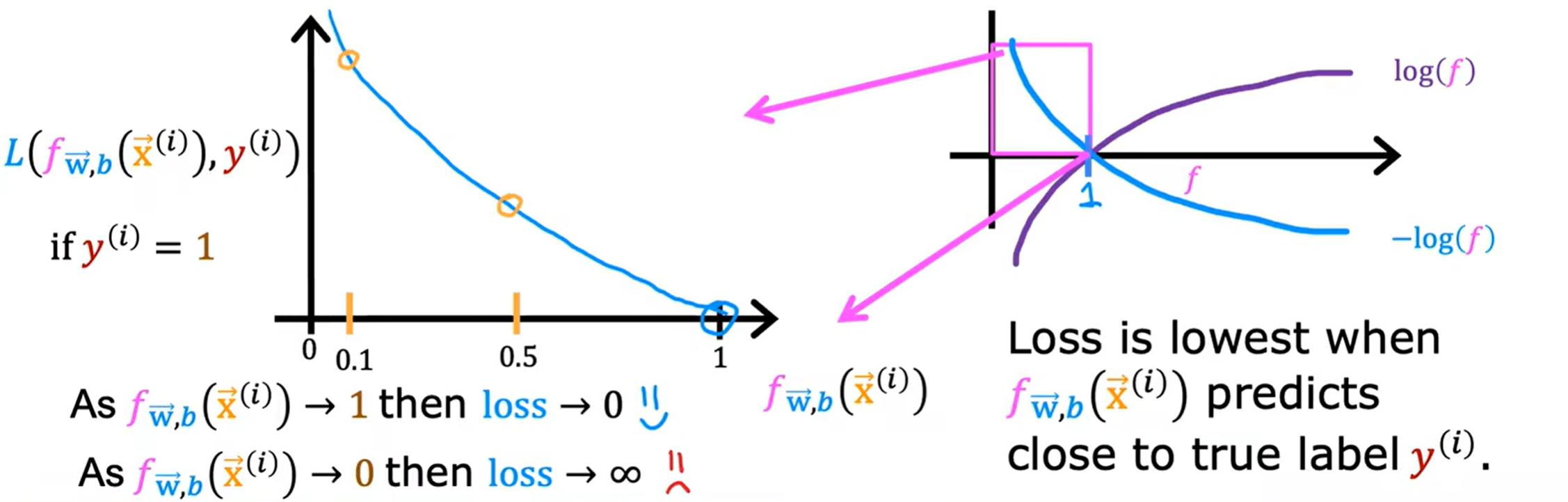  ### 代价函数(Cost Function) 逻辑回归的代价函数是所有训练样本损失函数的平均值,即 $\frac{1}{m}$ 乘以所有训练样本上损失的总和。逻辑损失函数产生的图形是一个漂亮而光滑的凸表面,没有那些局部最小值,因此,使用逻辑损失函数可以轻松地使用梯度下降法找到全局最小值,而不用担心陷入局部最小值。  ### 简化 ~ 损失函数(Simplified Loss Function) $$ f(x) = -y^{(i)}*log(f_{\vec{w},b}(\vec{x}^{(i)}))-(1-y^{(i)})*log(1-f_{\vec{w},b}(\vec{x}^{(i)})) $$ 逻辑回归模型的参数可以用梯度下降法来拟合,我们可以使用逻辑回归的损失函数来评估模型的表现。在这种情况下,目标标签 y 只能取 0 或 1 的值,因此可以使用一个更简单的损失函数表达式,即上面的公式。这个表达式等价于分段表示的逻辑回归损失函数,因此,我们可以用更简单的表达式来写损失函数,而不用分两类讨论。  ### 简化 ~ 代价函数(Simplified Cost Function) 使用简化的损失函数,可以更方便地计算逻辑回归模型的成本函数,逻辑回归的成本/代价函数是所有训练样本损失函数的平均值。逻辑回归的代价函数是一个凸函数,它可以使用极大似然估计的统计原理来推导。极大似然估计是一种统计学中用于寻找模型参数的方法,它可以用于逻辑回归中,以帮助寻找最优的模型参数。  ## 5.5 梯度下降 使用梯度下降算法最小化逻辑回归中的代价函数 $J$,我们需要对每个参数 $w_j$ 和 $b$ 执行更新操作,更新公式为旧值 - 学习率 α \* 偏导数项。需要注意的是,更新操作是使用同步更新的方法,即先计算更新右边的值,然后同时更新左边的值。  逻辑回归和线性回归算法虽然看起来相似,但它们的函数定义不同,因此它们是两个不同的算法。特征缩放也可以应用于逻辑回归中,加快梯度下降的收敛速度。  # 6、正则化解决过拟合 ## 6.1 欠拟合 & 过拟合(Underfitting & Overfitting) 欠拟合和过拟合是机器学习中常见的两种模型问题。欠拟合指的是模型无法很好地拟合训练数据,表现为模型在训练集和测试集上的误差都比较大,即模型无法很好地理解数据的规律。过拟合则指的是模型过于复杂,过度拟合了训练数据,表现为模型在训练集上表现很好,但在测试集上表现较差,即模型过度地记忆了训练数据的噪声和细节,而失去了泛化能力。 * **在欠拟合情况下,模型不能够很好地拟合数据集,因此无法捕捉数据中的模式。** * **在过拟合情况下,模型过于复杂,试图拟合数据中的噪声,从而导致对新数据的预测性能下降。**   **Underfitting → high bias (高偏差)** : 指模型对真实关系的错误假设或缺乏表示能力。 **just right → generalization (泛化)** : 指模型在未见过的数据上表现较好的能力。 **Overfitting → high variance (高方差)** : 指模型对训练数据的小变化非常敏感。 ## 6.2 解决过拟合(Addressing Overfitting) ### ① 增加训练样本(More Training Examples) 收集更多的训练数据是解决过拟合问题的首要工具,如果有更多的数据,算法可以更好地拟合数据,得到更稳定的函数,但如果没有更多的数据可用,则无法使用此方法解决过拟合问题。  ### ② 特征选择(Feature Selection) 特征选择是通过使用更少的特征来减少模型的过拟合问题,选择最合适的特征集有时也被称为特征选择,可以用直觉选择出最相关的特征集,但这可能会丢失其他有用的信息。  ### ③ 正则化(Regularization) 正则化是通过缩小参数的值来防止特征权重过大,进而解决过拟合问题,而不是直接消除特征,正则化可以保留所有的特征。通常只需要对参数 $w_j$ 进行正则化,对参数 $b$ 是否正则化没有太大差别。 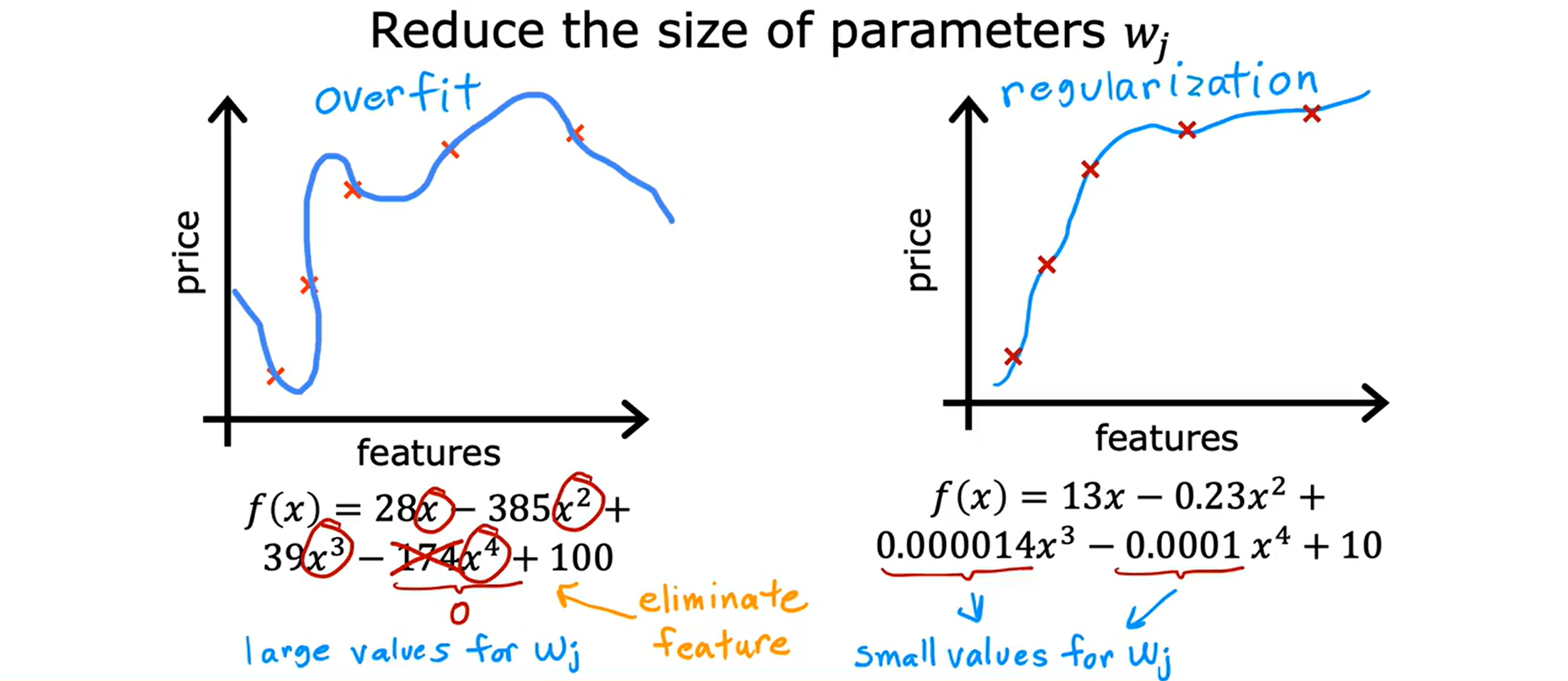 ## 6.3 正则化代价函数(Cost Function With Regularization) ### 惩戒部分特征参数 在高阶多项式拟合中,正则化是一种常用的方法,可以通过在代价函数中增加对参数的惩罚项来避免过拟合问题。正则化的核心思想是通过惩罚高阶项参数来降低高阶项对模型预测的影响,从而简化模型并使其更加健壮,同时获得更好的泛化性能。 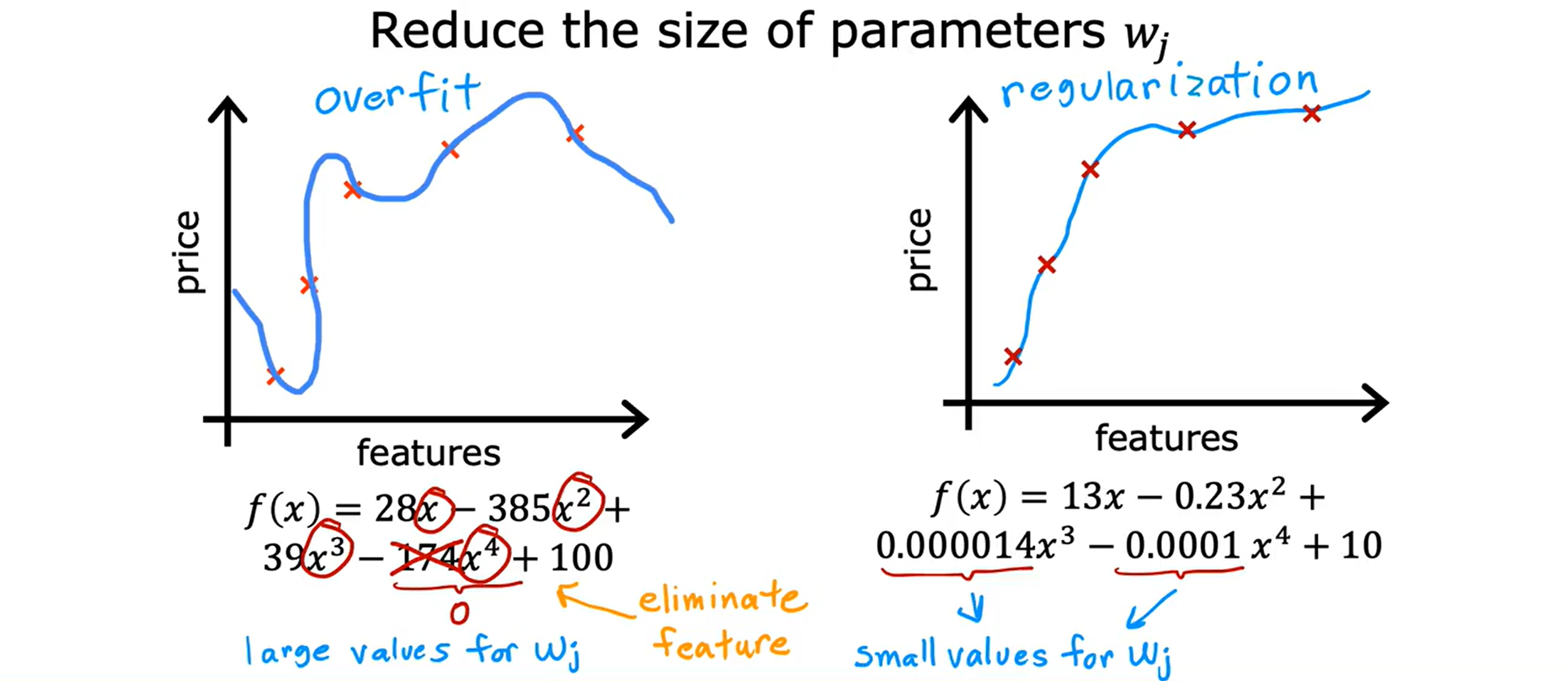 ### 正则化代价函数 在实际应用中,通常难以确定哪些特征是最重要的,因此常常对所有参数都进行惩罚,即将所有参数的平方和加入到代价函数中,并乘以一个正则化参数 $\lambda$,通过调节 $\lambda$ 的大小来控制正则化的程度。需要注意的是,在实现正则化过程中,通常会将惩罚项除以 2m,以便与均方误差项的量级相同,并且在选择 $\lambda$ 的值时,需要根据训练集大小 m 进行适当的缩放。对于偏置项 b,通常不会进行正则化处理,因为其对代价函数的影响相对较小。  ### 正则化参数 λ 的选择 选择合适的 $\lambda$ 值是为了平衡模型的拟合能力和泛化能力,$\lambda$ 值的大小会影响模型的复杂度和对数据的拟合程度。当 $\lambda$ 的值适中时,模型能够平衡拟合程度和复杂度,得到一个泛化能力较好的模型。这时模型会在保持拟合能力的同时,对过度拟合的特征进行惩罚,从而避免过拟合现象的发生。 * **如果 $\lambda=0$,那么模型没有正则化项,模型会过度拟合数据。** * **如果 $\lambda$ 很大,模型会过度依赖于正则化项,而减少对训练数据的拟合。**  ## 6.4 **线性回归的正则化** 线性回归的正则化与普通线性回归相比,只是代价函数 $J$ 的定义有所不同,正则化代价函数包括平方误差代价函数和正则化项,其中 $\lambda$ 是正则化参数。与普通线性回归相同,为了找到最小化正则化代价函数的参数 $w$ 和 $b$,我们需要使用梯度下降算法重复更新参数 $w_j$ 和参数 $b$。 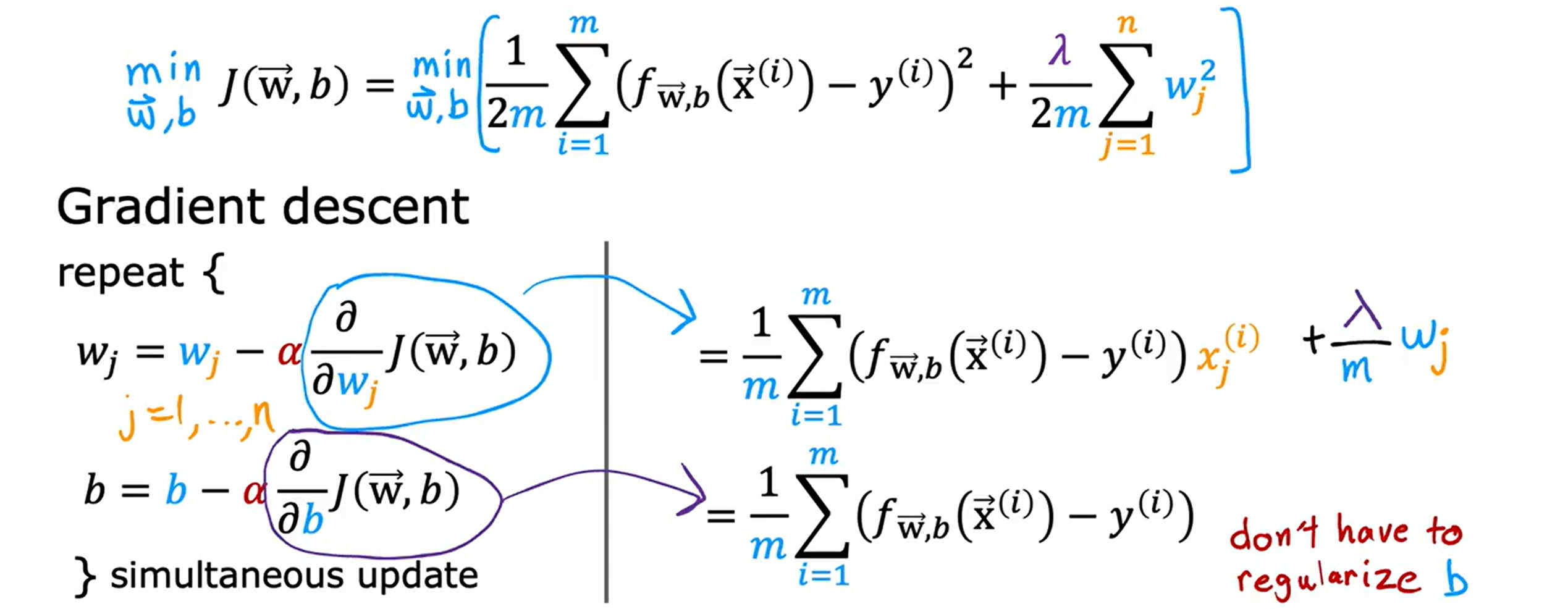 我们将 $w_j$ 的更新规则重新表示为 $w_j = w_j(1 - \alpha\frac{\lambda}{m}) - \alpha\frac{1}{m}\sum_{i=1}^{m}(f_{\vec{w},b}(x^{(i)})-y^{(i)})x_j^{(i)}$,与普通线性回归相比,更新规则相同前面的 $w_j$ 项多乘了 $(1 - \alpha\frac{\lambda}{m})$,经过分析我们可以知道 $(1 - \alpha\frac{\lambda}{m})$ 将会是一个略小于 1 的数,这意味着,正则化在每次迭代中将 $w_j$ 的值缩小了一些。  ## 6.5 **逻辑回归的正则化** 正则化逻辑回归的梯度下降更新与正则化线性回归的更新类似,需要在代价函数中添加一个额外的正则化项。正则化项表示为 $\frac{\lambda}{m}w_j$,其中 $\lambda$ 是正则化参数,$m$ 是训练样本的数量,$w_j$ 是特征的权重。逻辑回归的决策边界可以处理高阶多项式特征,并且通过正则化可以避免过拟合,同时只需对参数 $w_j$ 进行正则化,不需要对参数 $b$ 进行正则化。 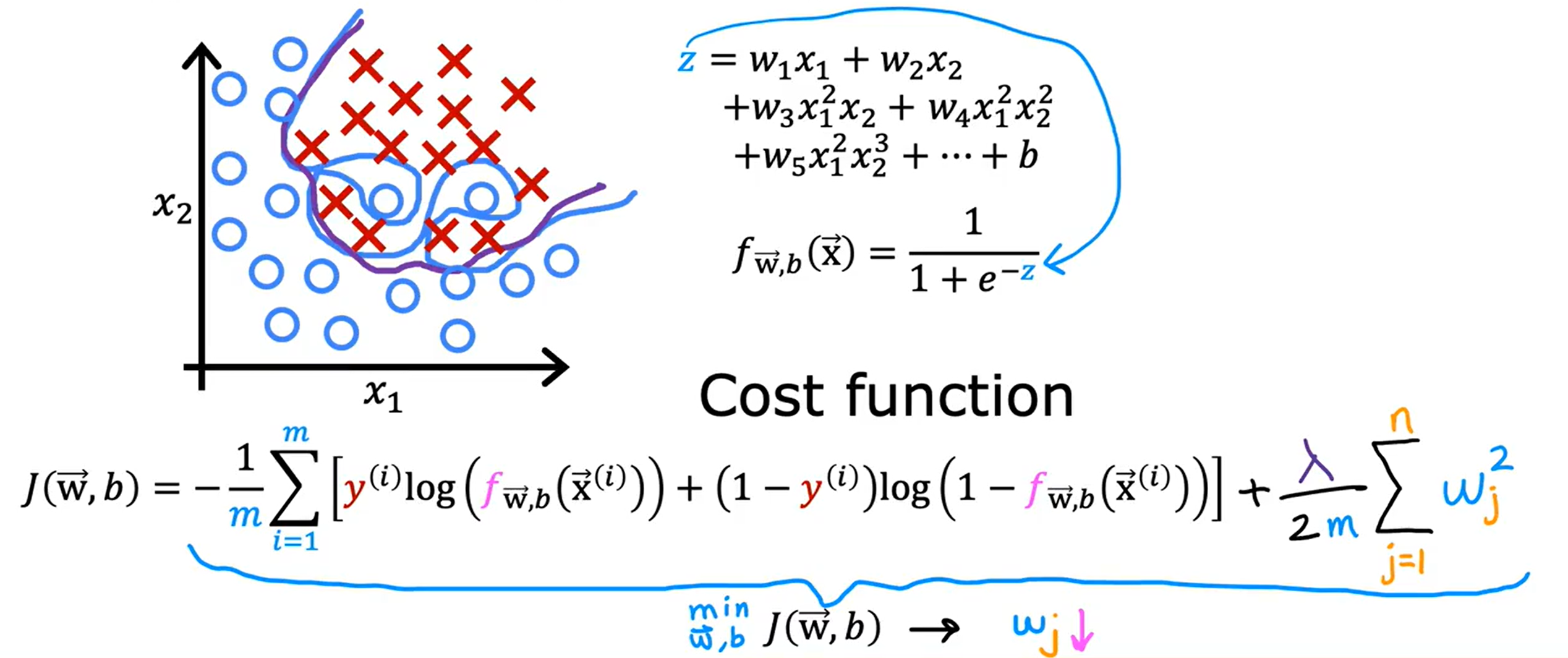 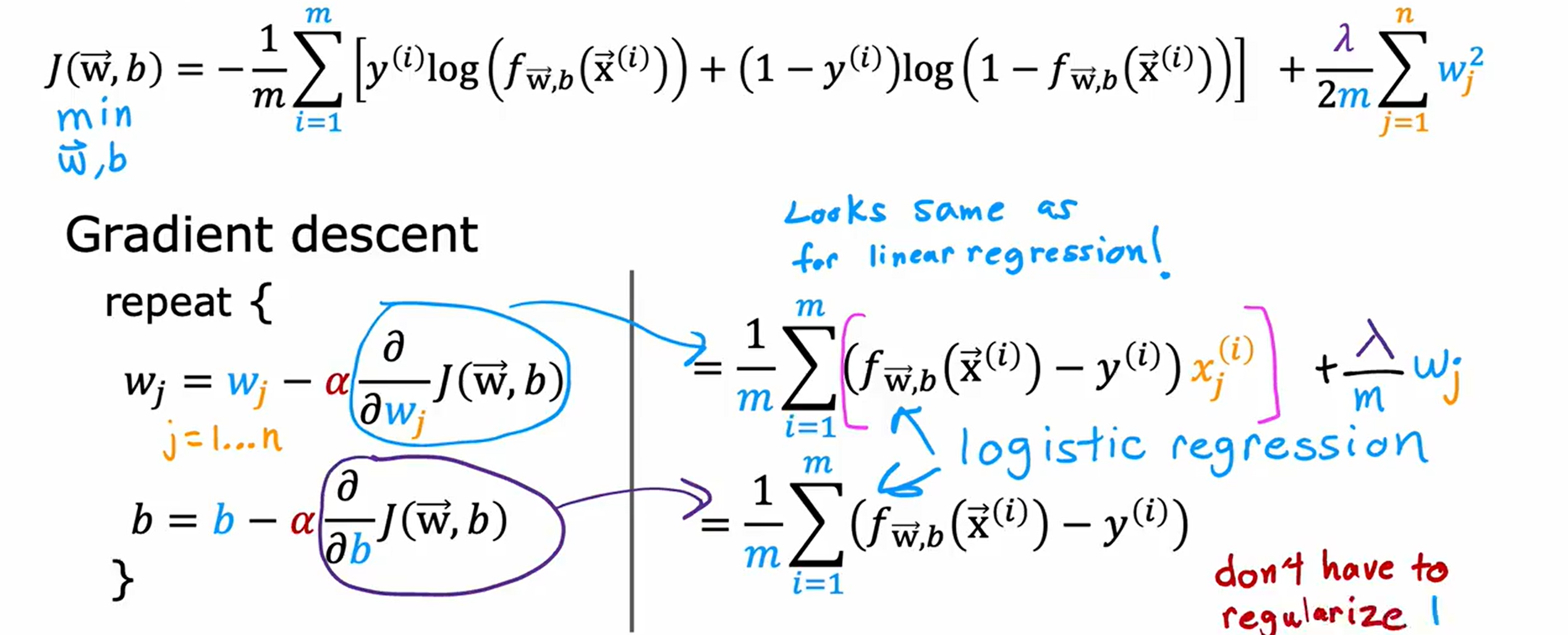 Last modification:August 8, 2024 © Allow specification reprint Support Appreciate the author AliPayWeChat Like 如果觉得我的文章对你有用,请随意赞赏
3 comments
情感真挚自然,字里行间传递出强烈的感染力。
文化符号解读精准,展现独特审美。
研究方法科学,数据支撑充分,结论可靠。